1. razred - Fizika
2. Kinematika
Kinematika uvod
Mehanika kao veliki deo fizike se deli na klasičnu mehaniku i kvantnu mehaniku.
-
klasična mehanika proučava mehaničko kretanje tela koja se kreću
brzinama koje su male u poređenju sa brzinom svetlosti u vakuumu
v ≪ c ≈ 3*108 m/s
uz proučavanje mehaničkog kretanja, proučava i uzroke (sile) koje su dovele do kretanja. Klasična mehanika se deli na:- kinematiku
- dinamiku
- statiku
- kvantna mehanika proučava zakone kretanja tela koja se kreću
brzinama
v ≈ c ≈ 3*108 m/s
koje su reda brzine svetlosti (Ajnštajnova mehanika).
Kinematika proučava kretanje tela ne razmatrajući uzroke koji su doveli do kretanja.
Dinamika proučava kretanje tela i uzroke koji su doveli do kretanja ili promene pri kretanju, odnosno proučava delovanje sila na tela.
Statika proučava ravnotežu tela kada na njih deluje nekoliko sila.
Mehaničko kretanje
Kretanje raznih objekata kao što su voz, biciklo, avion ili živih bića kao ptica, ljudi se dešava oko nas i ono može definisati kao kretanje u odnosu na neko drugo telo:
kretanje puža u odnosu na kornjaču

kretanje leptira u odnosu na cvet

Mehaničko kretanje je promena položaja jednog tela u odnosu na drugo u nekom vremenskom periodu (drugo telo se u ovom slučaju zove referentno telo, pošto se u odnosu na njega određuje kretanje).
Relativnost kretanja
Kretanje se uvek posmatra u odnosu na neko drugo telo. Telo u odnosu na koje se posmatra i opisuje kretanje, zove se referentno telo.
U prethodnom poglavlju se videlo kretanje puža u odnosu na kornjaču i kretanje leptira u odnosu na cvet.
Kretanje objekata u sunčevom sistemu u odnosu na sunce:
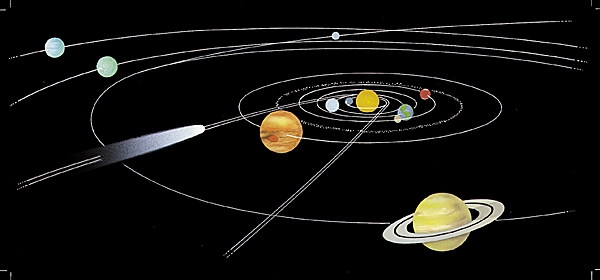
Kretanje bolida formule 1 u odnosu na stazu:

Kretanje bilijarskih kugli u odnosu na bilijarski sto:

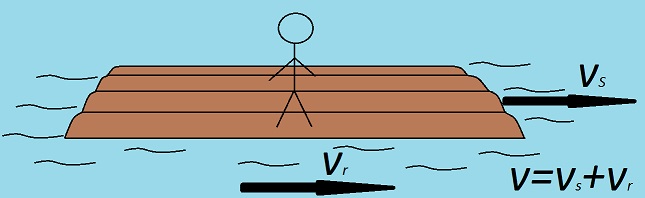
Čovek je u stanju mirovanja u odnosu na splav (iako se splav kreće), ali se u ovom slučaju posmatra kretanje čoveka u odnosu na splav:
Materijalna tačka
Ukoliko je putanja tela veoma velika u odnosu na dimenzije tela moguće je zanemariti oblik i dimenzije tela, te se to telo može posmatrati kao jedna materijalna tačka.

Na primer ukoliko se posmatra putanja automobila koja je dužine nekoliko kilometara a sam auto je dužine 4-5 metara, automobil se može posmatrati kao materijalna tačka.
Referentni sistem
Koordinatni sistem u čijem početku se nalazi referentno telo, naziva se referentni sistem.
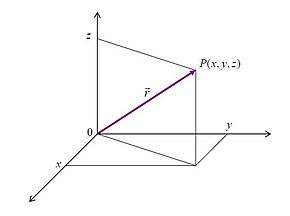
Vektor položaja
Vektor položaja tela je vektor koji spaja koordinatni početak i telo a usmeren je od koordinatnog početka ka telu.
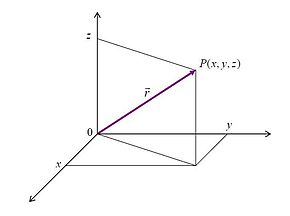
Intenzitet vektora položaja se računa na osnovu Pitagorine teoreme:
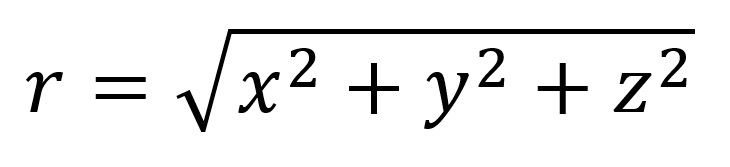
Putanja i put
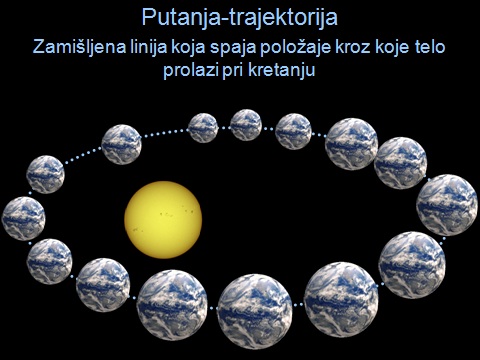
Tokom kretanja telo ili materijalna tačka neprekidno menja svoj položaj. Za kompletno razumevanje kretanja upotrebljava se pojam putanja.
Putanja je linija koju telo ili materijalna tačka opisuje tokom kretanja od početnog do krajnjeg položaja u datom referencijalnom sistemu.
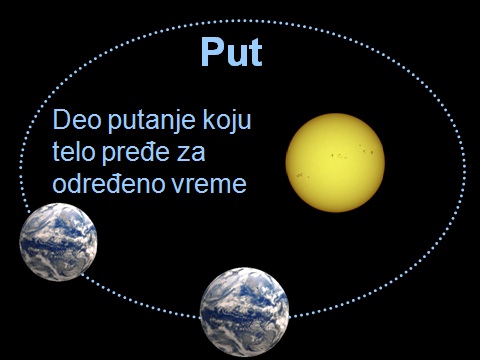
Put je deo putanje koji telo ili materijalna tačka pređe u određenom vremenskom intervalu.
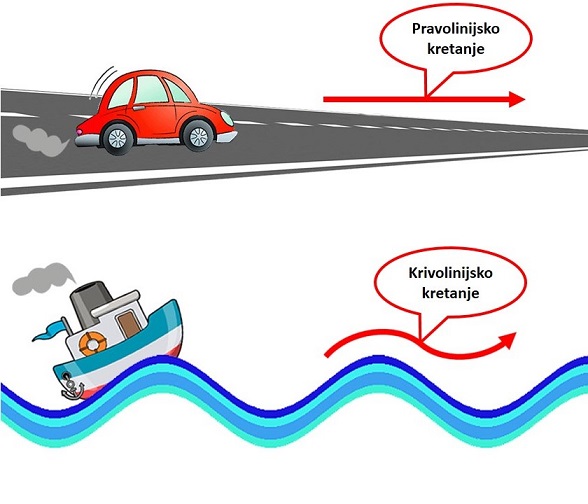
Zavisno od oblika putanje (puta), kretanje može biti:
- pravolinijsko
- krivolinijsko
Ravnomerno i neravnomerno kretanje
Pravolinijsko kretanje može da bude ravnomerno i neravnomerno. Kod ravnomernog pravolinijskog kretanja se telo ili materijalna tačka kreće stalnom brzinom. Kod neravnomernog pravolinijskog kretanja se telo ili materijalna tačka kreće različitim brzinama.
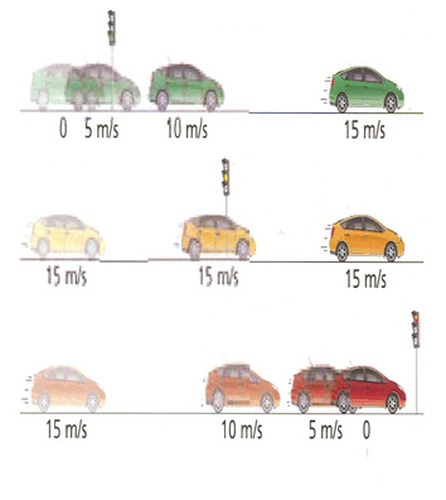
Na prethodnoj slici se žuti automobil kreće ravnomerno brzinom od 15km/h, dok se zeleni i crveno automobil kreću neravnomerno. Zeleni automobil ubrzava, dok crveni automobil usporava.
Pomeraj
Vektor pomeraja je vektor koji spaja vektore položaja u početnom i krajnjem vremenskom intervalu, na slici Δr⃗.
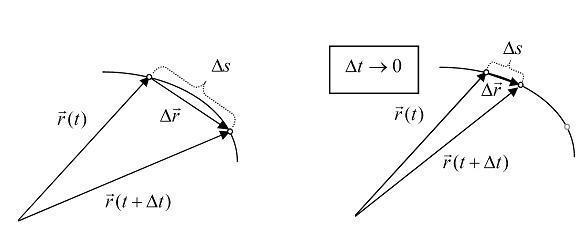
Brzina tela
Brzina opisuje razliku između tela koje se kreće i tela koje miruje. Definiše se kao odnos pređenog puta i vremena za koje se taj put prešao.
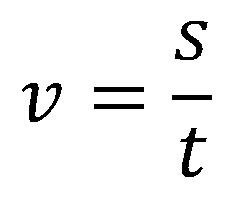
U prirodi je veoma redak slučaj ravnomernog pravolinijskog kretanja. Za slučaj krivolinijskog kretanja se upotrebljava formula po kojoj se putanja deli na kratke delove puta, a samim time se i vreme deli na kratke intervale.
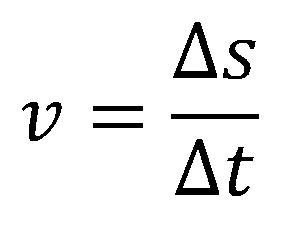
Brzina je vektorska veličina, poseduje intenzitet, pravac i smer. Pomoću prethodne formule se određuje samo intenzitet brzine. Za dobijanje sve tri komponente brzine potrebno je brzinu određivati na osnovu pomeraja.
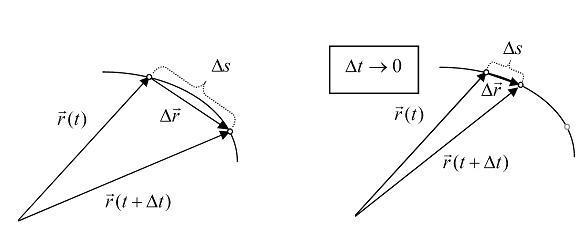
Na osnovu slike sledi da se brzina izražava kao:
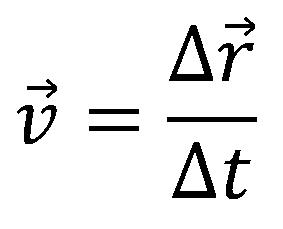
Ukoliko se putanja deli na veoma male delove, ova formula može da se primeni na složenije putanje kretanja tela. Intenzitet vektora brzine se računa kao odnos intenziteta vektora pomeraja i vremena u toku kojeg je pomeraj napravljen.
Srednja vrednost brzine
U svakodnevnom životu kretanja su neravnomerna, proizvoljna i veoma složena. Za proračune ovakvih kretanja se upotrebljava pojam srednja vrednost brzine. Srednja vrednost brzine je skalarna veličina.

Izračunavanje srednje vrednosti brzine se vrši na sledeći način:
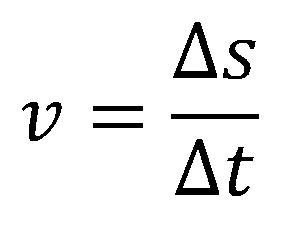
Srednja vrednost brzine je odnos pređenog puta i vremenskog intervala za koji je taj put pređen.
Trenutna brzina
Brzina tela u tački putanje u datom vremenskom trenutnku se zove trenutna brzina. Određuje se putem vektora pomeraja, kada vremenski interval teži nuli.

Klasičan zakon slaganja brzina
Klasičan zakon slaganja brzina koji povezuje referentne sisteme glasi:
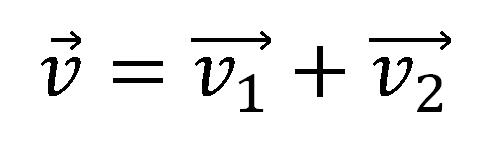
Na slici je prikazano kretanje reke vr i kretanje čoveka na splavu vs kao primer sabiranja brzina.
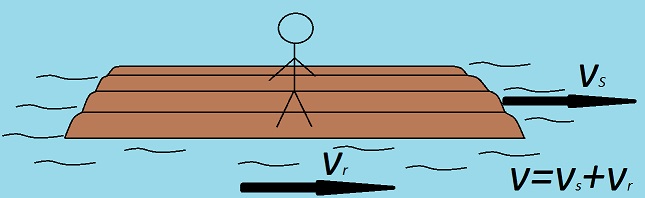
Najjednostavniji primeri ovakvog kretanja su kretanja putnika u vozilima koja se kreću.
Srednje ubrzanje
Promena brzine tela u toku vremena se zove ubrzanje tela.
Promena brzine Δv⃗ se dobija kao razlika vektora brzine Δv⃗ = v2⃗ - v1⃗.
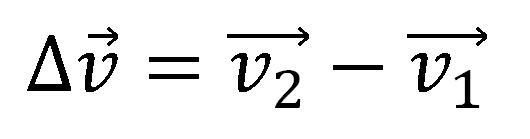
Vektor ubrzanja ima smer vektora razlike brzina (vektor promene brzine se deli sa skalarnom veličinom):
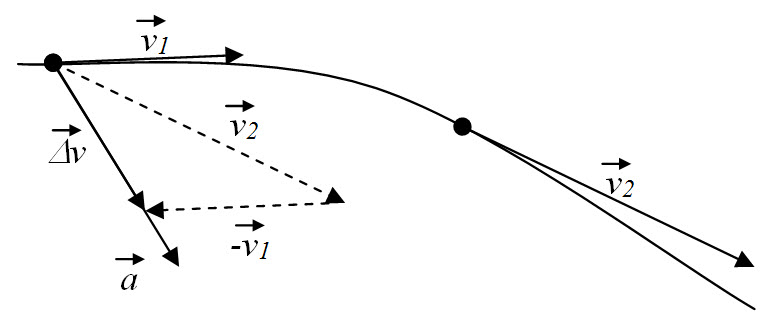
Srednje ubrzanje se definiše kao odnos promene brzine i vremenskog intervala u kome se desila ta promena brzine:
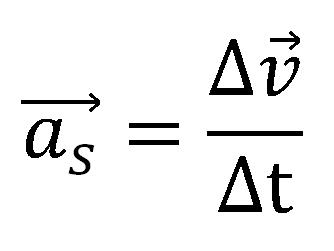
Može se napisati kao:
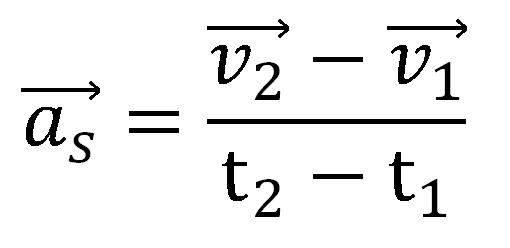
Intenzitet srednjeg ubrzanja je promena intenziteta brzine u jedinici vremena.
Trenutno ubrzanje
Trenutno ubrzanje je kada se vremenski interval svodi na veoma mali vremenski period (trenutak).
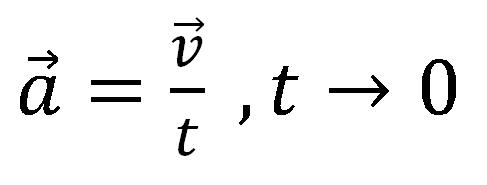
Radijalna (normalna) i tangencijalna komponenta ubrzanja
Kod krivolinijskog kretanja ubrzanje se razlaže na dve komponente ubrzanja: radijalnu (normalnu) i tangencijalnu.
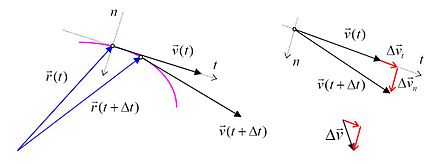
Zbir radijalne (normalne) i tangencijalne komponente ubrzanja daje vektor ubrzanja. Pravac tangencijalne komponente ubrazanja je tangenta na putanju. Pravac radijalne komponente ubrzanja je normalan na tangentu putanje i usmeren je ka centru krivine putanje.
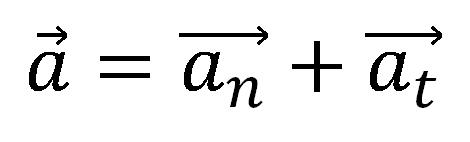
Radijalno ubrzanje određuje promenu pravca brzine, dok tangencijalno ubrzanje određuje promenu intenziteta brzine.
Ukoliko ubrzanje nema radijalnu komponentu kretanje tela je kružno.
Ukoliko ubrzanje nema tangencijalnu komponentu kretanje tela je pravolinijsko.
Ukoliko su poznate i radijalna i tangencijalna komponenta ubrzanja, intenzitet ubrzanja se određuje pomoću Pitagorine teoreme:
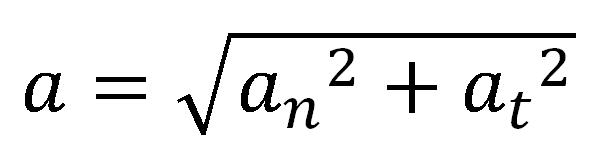
Ravnomerno i ravnomerno promenljivo pravolinijsko kretanje
Kretanje tela čija se brzina menja u toku vremena naziva se promenljivo (neravnomerno) kretanje. U prirodi se uglavnom sreće promenljivo kretanje.
Ukoliko je putanja tela prava linija, to kretanje se zove pravolinijsko kretanje. Ovo je i ujedno najjednostavniji oblik promenljivog kretanja.
Ukoliko se brzina tela ravnomerno povećava tokom vremena to kretanje se zove ravnomerno pravolinijski ubrzano kretanje.
Ukoliko se brzina tela ravnomerno smanjuje tokom vremena to kretanje se zove ravnomerno pravolinijski usporeno kretanje.
Ravnomerno ubrzano kretanje (bez početne brzine):
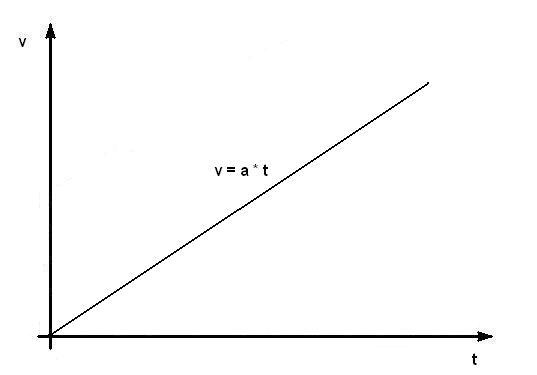
Ravnomerno ubrzano kretanje sa početnom brzinom:
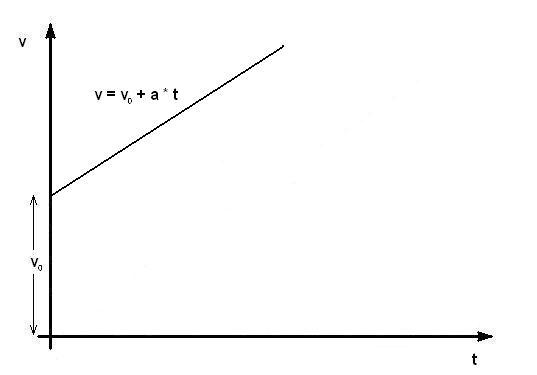
Ravnomerno usporeno kretanje:
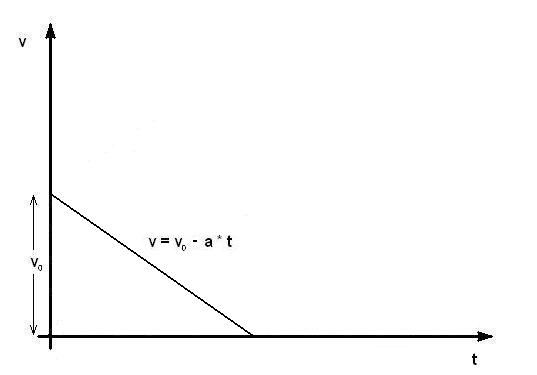
Izračunavanje ravnomerno promenljivog pravolinijskog kretanja:
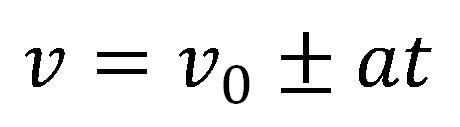
Pređeni put pri kretanju tela sa stalnim ubrzanjem
Pređeni put pri kretanju tela sa stalnim ubrzanjem se može odrediti grafički i on je jednak površini ispod grafikona zavisnosti brzine od vremena.
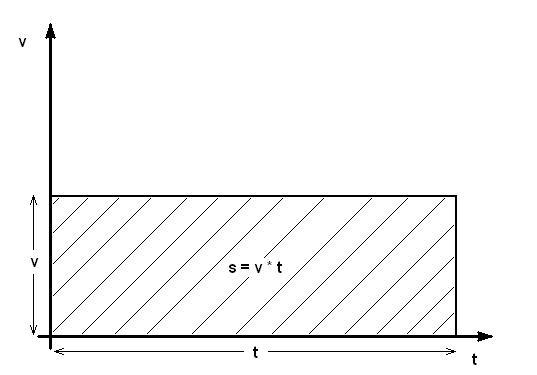
Ukoliko se telo kreće ravnomerno ubrzano, grafik izgleda na sledeći način, osim pravougaonika (koji predstavlja početnu brzinu v0), nalazi se i trougao koji predstavlja ubrzano kretanje. Povtšina trougla je osnovica (t) pomnožena sa visinom (t-t0) i podeljeno sa 2.
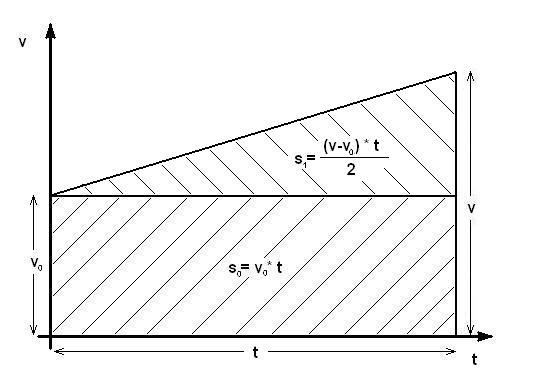
Na osnovu dijagrama se može napisati:
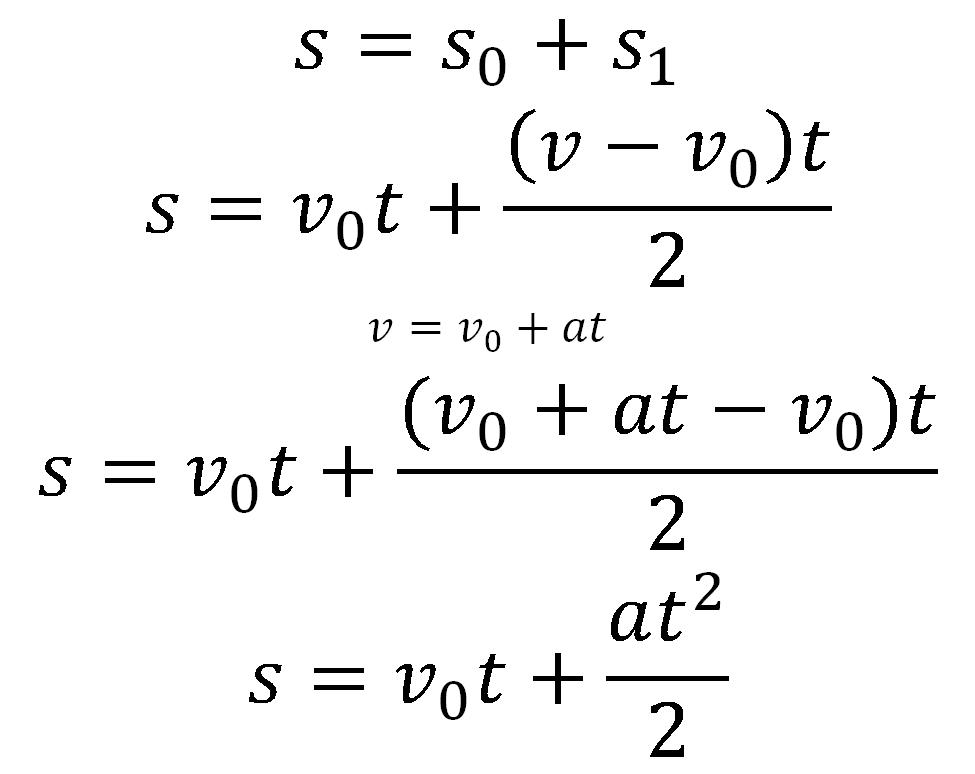
Pri čemu se za ravnomerno usporeno kretanje dobija izraz sa znakom minus u delu jednačine za ubrzanje. Na osnovu navedenog sledi zakon ravnomerno ubrzanog (usporenog) pravolinijskog kretanja:
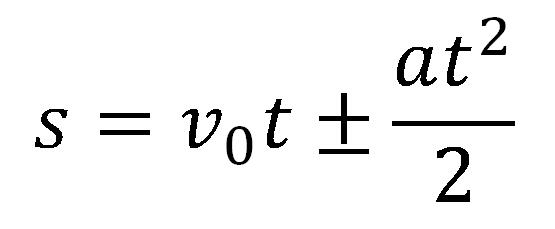
Zavisnost brzine od puta
Za rešavanje pojedinih zadataka potrebna je i sledeća relacija, u kojoj se brzina izračunava iz pređenog puta i ubrzanja. Ukoliko se kombinuju jednačine:
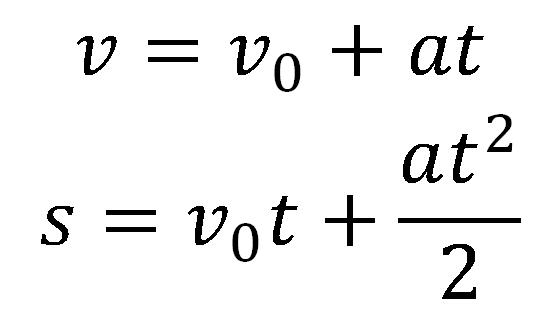
Iz prve jednačine se izražava t, i dobija se:
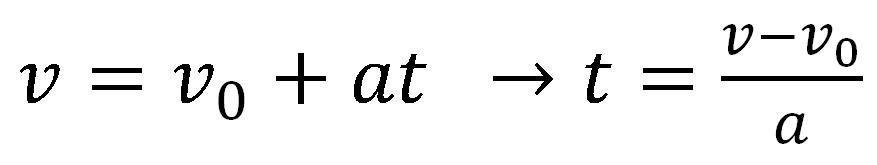
U drugu jednačinu se uvrštava t, i dobija se:
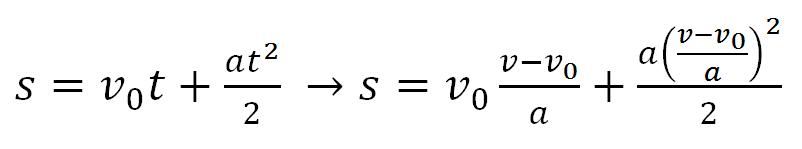
Sledi sređivanje jednačine:
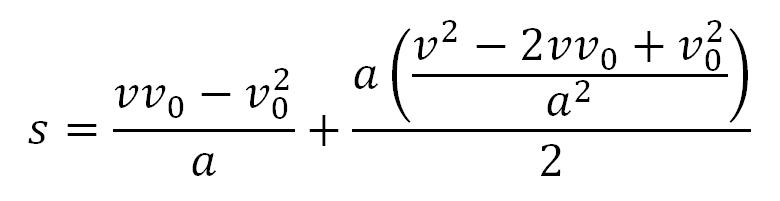
Daljnjim uređivanjem se dobija:
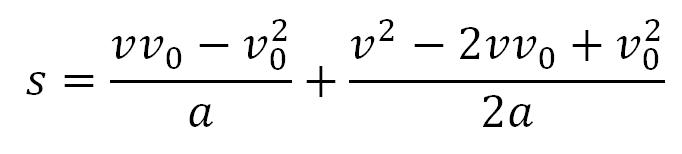
Sabiranje razlomaka:
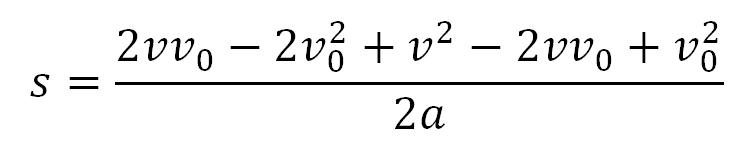
Uređivanje brojioca razlomka daje:
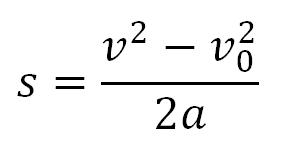
I sledi:
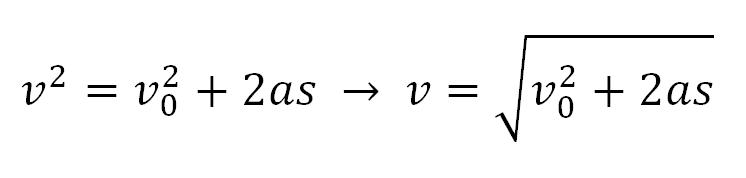
U slučaju da nije bilo početne brzine, sledi zavisnost brzine od puta:
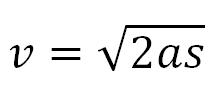
Kretanje materijalne tačke po kružnoj putanji
Najjednostavniji oblik krivolinijskog kretanja je kružno kretanje.
Kružno kretanje nastaje kada je tangencijalna komponenta ubrzanja jednaka nuli i postoji samo normalna odnosno radijalna komponenta ubrzanja.

Kružno kretanje poseduje pomeraj, put i ubrzanje. Za ovaj način kretanja se upotrebljavaju izrazi kao što su ugaoni pomeraj, ugaona brzina i ugaono ubrzanje.
Ugaoni pomeraj i opisani ugao
Pomeraj na kružnici se određuje pomoću vektora položaja - radijus vektora. Taj vektor spaja centar kružnice koja opisuje putanju i dato telo koje se kreće. Pri kretanju radijus vektor opisuje određeni ugao, odnosno pravi ugaoni pomeraj.
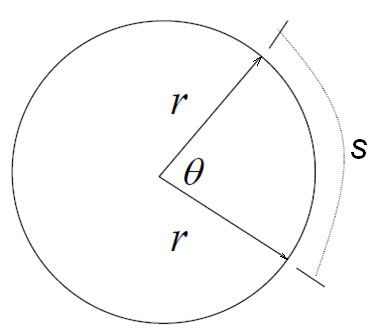
Ugaoni pomeraj j ugao između početnog i krajnjeg radijus vektora.
Ugao u radijanima je količnik dužine kružnog luka i poluprečnika kružnice.
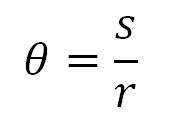
Pun ugao u stepenima je 360o, dok je u radijanima (putanja s koja opisuje pun krug, jednaka je obimu kruga 2rΠ):
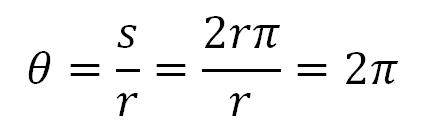
Uglovi izraženi na ovaj način imaju za jedinicu mere radijan [rad].
Put (dužina luka) je jednaka proizvodu poluprečnika kruga i ugla.
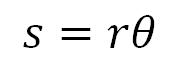
Ugaona brzina
Srednja vrednost ugaone brzine je odnos promene ugla i vremena za koje se promena ugla dešava.
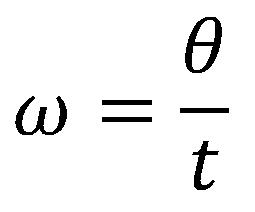
Trenutna vrednost ugaone brzine se dobija ukoliko vremenski interval t teži nuli
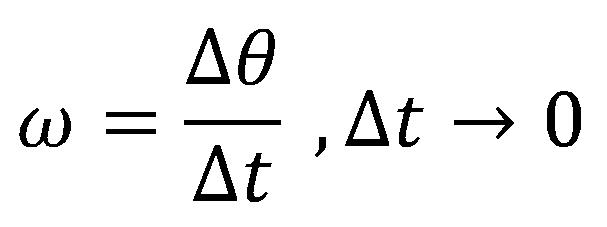
Ove veličine se mogu uočiti sa sledeće slike:
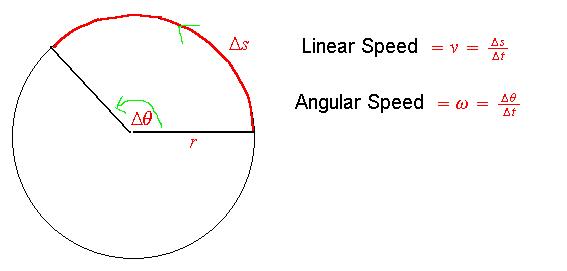
Jedinica mere ugaone brzine je [rad/s]
Veza između brzine i ugaone brzine
Ukoliko se krene od definicije ugaone brzine i opisanog ugla:
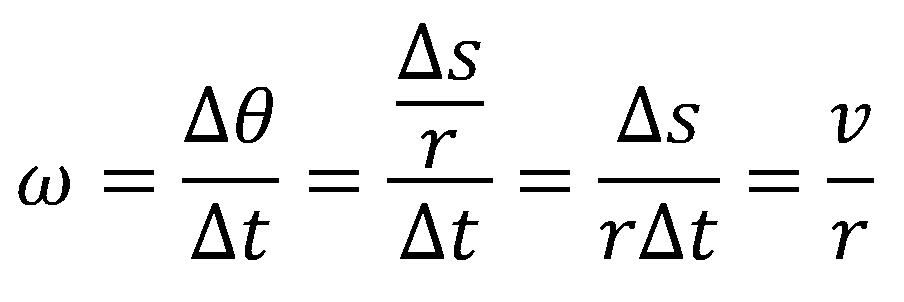
Dolazi se do veze ove dve veličine:
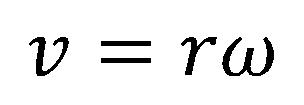
Periferijska (linijska) brzina tela koje se kreće po kružnoj putanji je jednaka proizvodu poluprečnika kružnice i ugaone brzine.
Ugaono ubrzanje
Kružno kretanje može da bude ravnomerno i promenljivo. Kod ravnomernog kružnog kretanja ugaona brzina se ne menja (ima stalnu vrednost). Kod promenljivog kružnog kretanja ugaona brzina se menja tokom vremena. Ukoliko se ugaona brzina menja, pojavljuje se ugaono ubrzanje
Srednje ugaono ubrzanje je odnos promene ugaone brzine i vremena u kojem je promena nastala.
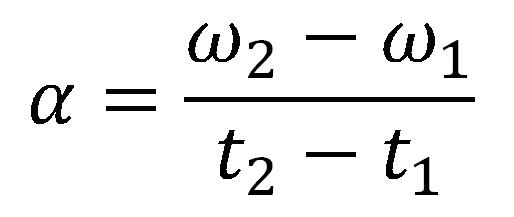
Trenutno ugaono ubrzanje je odnos promene ugaone brzine i vremenskog intervala u kojem je ta promena nastala, sa time da se posmatra što kraći interval vremena, odnosno interval vremena teži nuli.
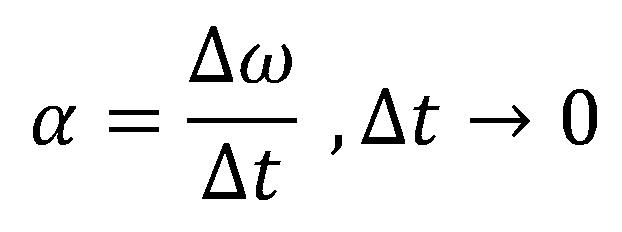
Jedinica mere ugaonog ubrzanja je [rad/s2]
Veza tangencijalnog i ugaonog ubrzanja
Telo koje se kreće kružnom putanjom sa promenljivom ugaonom brzinom, poseduje i tangencijalno ubrzanje.
Tangencijalno ubrzanje se dobija posmetranjem linijske i ugaone brzine:
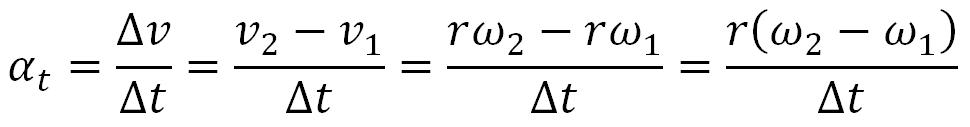
Na osnovu čega se može napisati:
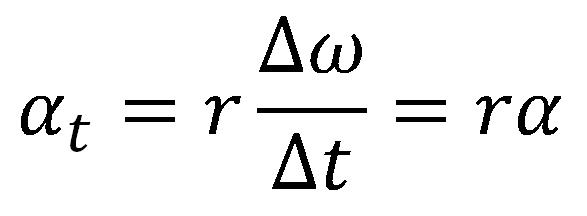
Ravnomerno kružno kretanje
Kod ravnomernog kružnog kretanja ugaona brzina je konstantna ω = const.
Period i frekvencija
Ravnomerno kružno kretanje je periodično kretanje (telo pri ravnomernom kružnom kretanju će uvek za isto vreme opisati jedan krug). Vremenski interval za koji će telo opisati jedan krug je period. Primera za ovo kretanje u svakodnevnom životu ima veoma mnogo.
Kod ravnomernog kružnog kretanja intenzitet brzine tela je:
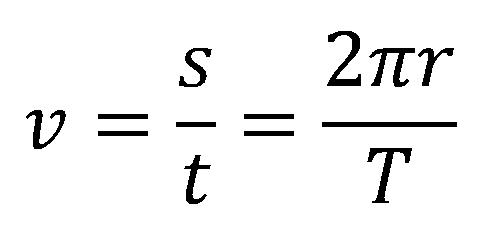
Period kružnog kretanja (vremenski period za koji telo opiše jedan krug):
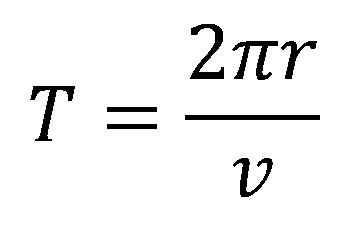
Veličina koja se naziva učestanost predstavlja koliko puta telo tokom vremenskog perioda opisuje jedan krug. Učestanost se drugim imenom naziva frekvencija. Obeležava se sa malim grčkim slovom ni (v) ili malim latiničnim slovom f.
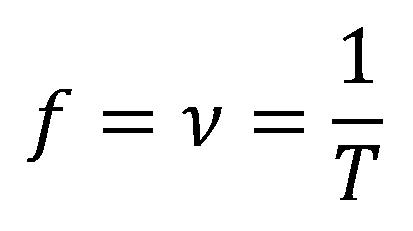
Jedinica mere za frekvenciju je Herc [Hz].
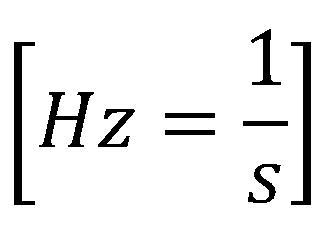
Telo koje obiđe pun krug u toku jedne sekunde ima frekvenciju od jednog herca.
Centripetalno (normalno) ubrzanje
Linijska (periferijska) i ugaona brzina pri ravnomernom kružnom kretanju imaju konstantne vrednosti, tangencijalno i ugaono ubrzanje je jednako nuli. Istovremeno se neprekidno menja pravac brzine, te postoji normalno ubrzanje.
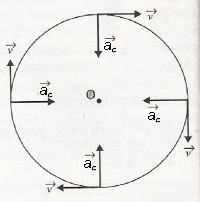
Kod kružnog kretanja normalno ubrzanje je usmereno duž poluprečnika ka centru kruga, usled toga se naziva radijalno ili centripetalno ubrzanje.
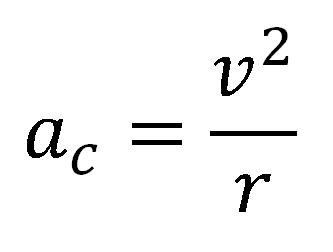
Translatorno i rotaciono kretanje
Kretanje pri kojem se sve čestice tela kreću po paralelnim putanjama zove se translatorno kretanje (lift, auto, ...).
Kod translacionog kretanja je dovoljno poznavati kretanje bilo koje tačke tela (pošto se sve tačke kreću na identičan način).
Rotaciono kretanje tela oko nepokretne ose
Kretanje skazaljki časovnika, kretanje propelera, kretanje točkova, predstavlja rotaciono kretanje.
Kretanje pri kojem se čestice tela kreću po koncentričnim kružnicama koje leže na međusobno paralelnim ravnima a centri tih kružnica leže na osi rotacije, naziva se rotaciono kretanje.
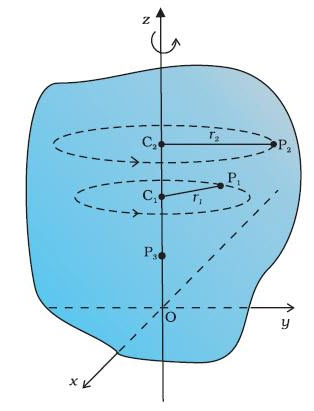
Telo koje pri kretanju ne manja oblik (čiji delići tokom kretanja ostaju u istim međusobnim položajima), zove se kruto telo.
Sve tačke tela za isto vreme opisuju iste uglove, odnosno imaju jednake ugaone pomeraje.
Ugaoni pomeraj i opisani ugao
Ugaoni pomeraj je ugao između početnog i krajnjeg radijus vektora bilo koje tačke tela.
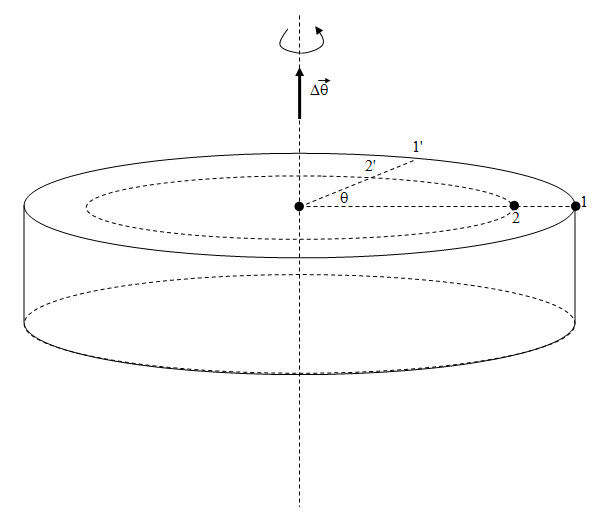
Opisani ugao je ukupan ugao kojeg opisuje radijus vektor bez obzira da li se u međuvremenu, tokom kretanja menjao smer rotacije (slično pređenom putu kod translacionog kretanja).
Vektorska priroda ugaonog pomeraja
Ugaoni pomeraj je vektorska veličina (kao što je i pomeraj pri translacionom kretanju vektorska veličina).
Ugaoni pomeraj za rotaciju tela oko nepokretne ose:
- intenzitet je jednak uglu između početnog i krajnjeg radijus vektora jedinica mere [rad]
- pravac vektora ugaonog pomeraja je pravac ose rotacije
- smer vektora ugaonog pomeraja se određuje pravilom desne ruke
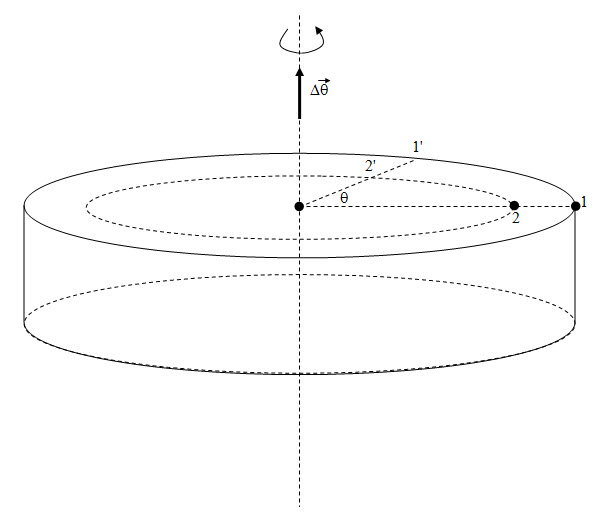
Smer vektora se određuje pravilom desne ruke, pri čemu prsti pokazuju pravac rotacionog kretanja a palac pokazuje smer vektora ugaonog pomeraja.

Ugaona brzina
Ugaona brzina je vektorska veličina i ima isti pravac i smer kao i ugaoni pomeraj.
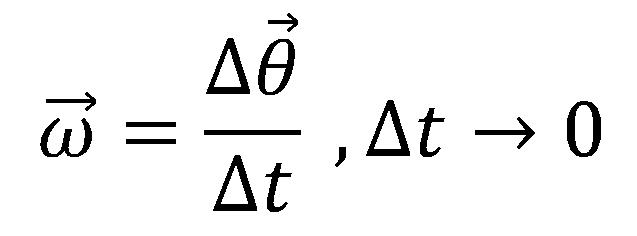
Intenzitet ugaone brzine se računa kao:
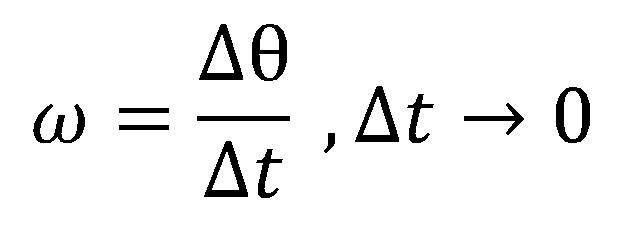
Jedinica mere za ugaonu brzinu je radijana u sekundi [rad/s].
Ugaono ubrzanje
Srednje ugaono ubrzanje je odnos promene ugaone brzine i vremenskog intervala u kome se ta promena desila.
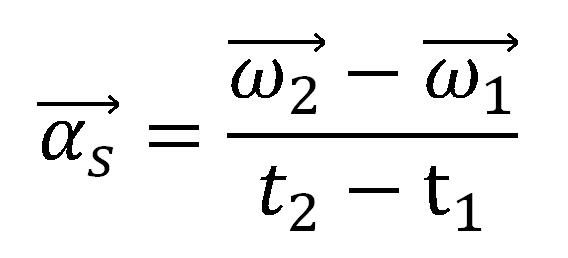
Trenutno ugaono ubrzanje ili ugaono ubrzanje je:
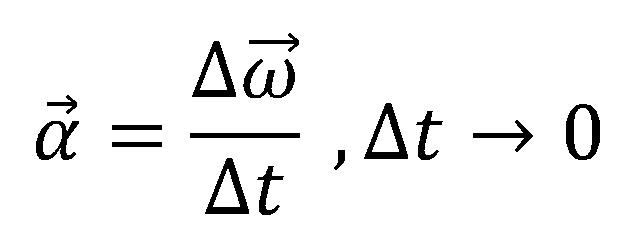
Jedinica mere je radijan u sekundi na kvadrat [rad/s2].
Analogija translatornog i rotacionog kretanja
Pregledi analognih veličina koje postoje pri translatornom i rotacionom kretanju su dati u sledećoj tabeli:
| Kinematika | |
|---|---|
| Translaciono kretanje | Rotaciono kretanje |
| put (s) | opisani ugao (θ) |
| pomeraj (Δr⃗) | ugaoni pomeraj (Δθ⃗) |
| brzina v⃗=Δr⃗/Δt | ugaona brzina ω⃗=Δθ⃗/Δt |
| ubrzanje a⃗=Δv⃗/Δt | ugaono ubrzanje α⃗=Δω⃗/Δt |