4. osztály - Fizika

Einstein a kezdőknek

Az emberi civilizáció kezdete óta általános aggodalmat jelentett az embereknek az ételek és a feltételek biztosítása az élethez. A számtalan hétköznapi problémák ellen elég nehéz találni olyan emberi fajt, amelyik valaha is élt ezen a földön és nem tette volna fel a kérdést magának az életről és a létezéséről. Minden embernek ismert, hogy minden esemény a természetben egy bizonyos helyen játszódik le, egy bizonyos időben és legtöbbször ugyanazon vagy hasonló módon. Minden reggel felkel a nap keleten, napközben utazik a kék égen nyugat felé, ahol este lenyugszik, este ugyanezen az égen utaznak a csillagok, tavasszal a növények zöld leveleket kapnak, ősszel ugyanezek a levelek besárgulnak és leesnek a földre. Ezek a történések a régmúltban is lejátszódtak az őseink idejében, de mindez ma is megtörténik. Minden ember naponta használja a tér és az idő fogalmát, amikor a saját terveikről beszélnek, a pillanatnyi munkájukról, vagy arról, hogy mit csináltak valamikor. Első ránézésre ez mind érthető, de ha valakit megkérdeznénk, hogy mi az a hely, és mi az az idő, akkor nehéz lenne rá választ adni, és a megkérdezett személy egy nagy probléma előtt találná magát.

Az első ember, aki megpróbálta megérteni a természetet, a helyet, az időt, a törvényeket, a természetet, Arisztotelész volt, i.e. a harmadik században. Arisztotelész tanítása nemis hasonlított arra, ahogyan ma leírjuk a természetet, és annak jelenségeit. Azt hitte hogy a természet körülöttünk és az összes törvényei leírhatók egyszerü gondolkozással és követkesztetéssel, ellenörzés nélkül a gyakorlatban. Hosszú megfigyeléssel és gondolkozással a természetre, fontos törvényekre és ötletekre jutott.

Azt állította hogy a világ négy elemből áll: földből, vízből, tűzből és levegőből, minden mozgás a természetben hatással volt arra hogy ezek az elemek elfoglalják saját helyüket a természetes feltételben. Hitt abban hogy a testek azért esnek a Földre mert az "természetes" viselkedés, a föld ábrázolja az ők természetes helyzetét, az volt a helyük ahol tartoztak, azért az volt az írányuk. Tűz esetén Arisztotelész hitte hogy a füst, amely többnyire levegőből áll, törekszik a saját természetes helyzetére, azaz levegőjére, azért is távolodik a földtől, azaz felfelé halad. Arisztotelész tanulmányaiban áll hogy a természetes helyzete a testnek egyben a nyugvás pozicíója. Minden test mozdulatlan ameddig egy erö azt nem váltosztatja (Arisztotelész az erő fogalmát nem használja mint a mai beszédben, mint az interakció a testek között, mármint azt állitja hogy az erő egy "vágy" egy testnek a saját természetes pozicíójához). Arisztotelész törvényei szerínt a nehezebb testek gyorsabban esnek mint a könyebbek mert nagyobb volt a "vágyuk" a természetes pozicíójukhoz, azaz a föld felé.

Arisztotelész összeálitott néhány átalános törvényt a mozgásról, de nem úgy álitotta mint ahogy a mai világban csinálják, matematikai képletek használatával, hanem a saját ötleteit és törvényeit kitette egyszerű nyelven amit minden ember használt.

Arisztotelész fizikai törvényei így szólnak:
I törvény (inercíó törvénye) - Minden test amelyre nem hat semmilyen erő, abszolút nyugalomban van.
II törvény (mozgás törvénye) - Az erő arányos a sebességgel (F=mv)
III törvény (gravitácíó törvénye) - A nehezebb testek gyorsabban esnek mint a könyebbek

A híres munkájában "A mennyben" Arisztotelész írt arról, hogy a Föld nem lapos lemez, hanem kerek, és sikerült kiszámítania viszonylag pontos körét. Ráadásul Arisztotelész közzétette az első modellt a világegyetemről - középen állt a Föld és a Nap, a Hold, a bolygók és a csillagok keringtek körülötte.

Arisztotelész idejében, és sok évszázaddal később is Arisztotelész törvényei sérthetetlenek voltak. Senki sem kételkedett a pontosságában, és nem is történt olyan, hogy valaki megpróbálta ellenőrizni a fizika törvényeit. Amikor először merült kétségek helyességében Arisztotel tanításában, valaki először a tanulmányát a világrol kísérletezett és kétség esett Arisztotel tanitásában.

Szerencsére, egy nap, egy ember született, akinek volt bátorsága, hogy azt állítsa, hogy az emberiség évszázadok óta tévhittben élt. Az az ember Galileo Galilei volt. Olaszországban született 1564-ben, ugyanabban az évben, mint Shakespeare, és akkor halt meg, mikor Michelangelo. Egyetemen egészségügyet tanult, de sohasem fejezte be. Az egész életét más tudományoknak szentelte, a fizikának és a csillagászatnak. Valószínűleg az ő nevéhez fűződik a fizika történelem legnagyobb találmánya. Ő volt az első, aki megértete a kísérletek fontosságát, és elkezdett különféle kísérleteket végezni azzal a szándékkal, hogy ellenőrizze Arisztotelész törvényeinek igazságát.

Az első dolog ami zavarta Arisztotelész törvényeiben, hogy a nagyobb tömegű testek gyorsabban esnek a kisebb tömegű testeknél, és Galilei ezt a törvényt ellenőrizni akarta kísérlettel. Valószínűleg mindenkinek ismert a történet Galileiről és a Pizai ferdetoronyról. Sokan elhiszik, hogy valóban véghez vitte ezt a kísérletet, viszont sokan vannak ez ellen, akik azt mondják, hogy a golyókat nem a toronyról, hanem egy meredek felületről engedte le. Nehéz eldönteni, hogy kinek van igaza, de elképzelhető, hogy mind a két állítás igaz. Stillman Drake volt az az ember aki eldöntötte, hogy életrajzot kell írni Galileóról, mert érdekes gondolatai vannak erről a kísérletről. Tulajdonképpen észrevette, hogy Galilei a tudományos kísérleteit különböző tömegű, de ugyanolyan méretű golyókat gurított le meredek lejtőkön. Ez a helyzet ugyanaz, mint a tárgyak ledobálása a torony tetejéről, de könnyebb megfigyeléseket végezni így a kisebb sebességnél. Galilei mérése megmutatta, hogy minden test arányosan növeli meg a sebességét attól függetlenül, hogy milyen a tömege illetve, hogy a test gyorsulása nem függ a tömegtől. Amikor a kísérletet többször megismételte, és teljesen biztos volt abban, hogy a munkának már csak a "könnyebb" része maradt hátra, meg kellett győzni a többi embert, hogy Arisztotelész tévedett. Galilei tudta, hogy az egyetlen módszer hogy bemutassa a kísérleteit, az hogy demonstrálja azokat (nincs jobb módszer hogy meggyőzze az embereket annál, hogy saját szemükkel lássák azt) és ehhez a bemutatáshoz szolgált a ferde torony. Természetesen Galilei nem lehetett benne teljesen biztos, hogy mi fog történni a nyilvános előadás előtt. Lion Lederman a könyvében erről írt:

Akárhogy is, Galileo biztosan tudta, hogy mit csinál, és képes volt meggyőzni az embereket, hogy Arisztotel tévedett ebben az esetben.

A következő dolog, ami zavarta Galileót Arisztotel tanításában a világegyetem geocentrikus modellje volt, azaz a Földnek a kiváltságos helyzetét. A teleszkóp használatával, amelyet ő szerkesztett, sikerült észlelnie kis objektumokat amelyek Jupiter körül keringtek (ma már ismert, hogy azok a testek valójábana Jupiter legnagyobb műholdai, amelyek az úgynevezett Galilei műholdai). Ez elég volt Gaileinek hogy rájöjjön arra hogy nem minden a Föld körül kerinng. Mivel evvel "támadta" Arisztotel tanulását, Galilei egy nagy probléma előtt találta magát, összeütközésbe került az Egyházzal és az inkvizícióval. Kénytelen volt visszavonni tanítását és így megmentette magát Giordano Bruno sorsátol, és nem lett a tűzbe vetve.

Megmentette az életét de nem a szabadságát is, a hátralévö éveit börtönben töltötte.

Elhunyt mint fogoly a saját házában 1642-ben, ugyan abban az évben Londonban született Isaac Newton.

Isaac Newton mindenkinek jól ismert név és minden amit csinált. A fejlődést amit ez az ember hozott a fizikába, és mondhatni, az emberi civilizációba megfizethetetlen. Minden bizonnyal mindenki jól emlékezik az általános iskolából, az első a fizika órájárol és három Newton-törvényeiröl: A tehetetlenség törvénye, a dinamika alaptörvénye és akció-reakció törvénye. Sokan hallottak már Newton történetét ahogyan ült egy fa alatt, és a leghíresebb almárol a világon, ami a gravitáció törvényéhez vezetett. A gravitáció törvénye, mondhatni, az első egyesítése a fizikával, azzal a törvényel Newton kimutatta, hogy ugyan az az erő felelős a hulló almákra, a levelekre, a Hold és a bolygók mozgására. Nehéz írni egy olyan emberröl, mint Newton volt, lehetetlen leírni a jelentőségét a felfedezéseiröl. Ahogy sétálunk az utcán, utazunk autóval, vonattal, repülővel, míg az űrhajósok utaznak az ürbe, és közben űrhajókat más bolygókra küldik, Newton törvényei "végzik munkáikat" és "ellenőrzik a helyzetet."

Valakinek meglehet hogy úgy tűnik hogy Newton elérte a tökéletességet fizikában de nem így van. Sok idő telt el amióta Newton ezeket a törvényeket felállította, és mi folyamatosan alkalmazzuk őket, de a XIX évszázad végén és a XX évszázad elején megjelentek egyes természetbeli helyzetek melyeket nem lehetett a Newton törvényeivel alapján magyarázni és leírni, és a fizika a további fejlődés útjára lépett.

A relativitás elméletének kezdetei

Arisztotelész, Galilei és Newton is hittek az abszolút időben. Hittek benne, hogy lehetséges megmérni az intervallumot két esemény között, illetve függetlenül attól, hogy ki méri az időt, csak egy jó órát használjon. Az idő önálló és független volt a tértől. Legtöbb ember szerint ez egy józan nézőpont volt. Mindazonáltal, az embereknek idővel meg kellett változtatniuk a nézőpontjukat a térrel és az idővel kapcsolatban.

Ötlet a mozdulatlan éterről

Sok évvel a fény gyorsaságának pontos mérése előtt ismert volt, tudták hogy a hangnak a terjedése, mechanikai hullámnak szüksége van egy tér létezésére, amelyen keresztül áthalad. A tér létezése azért szükséges, mert a hullámok az egyik részecskéről a másikra rezegve terjednek. Ismert volt, hogy a tér létezésének szükségességének hatására a hanghullámok nem terjedhetnek vákumban, ami a későbbiekben kisérletekkel alá lett támasztva. Más fajta, mindenkinek ismert hullámok, a vizi hullámok terjedésére víz volt szükséges. Mindezek után, teljesen érthető, hogy úgy tartották hogy a fény terjedéséhez, illetve az elektromágneses hullámok terjedéséhez, szükség van egy tér létezésére, illetve léteznie kell valami közegnek amelynek a részecskéi vibrálnának és igy vinnék át a fény hullámokat.

Az ötlet, hogy létezik valami anyag amely kitölti az egész unuverzumot ellenére, megbizhatóan tudták, hogy a hatalmas végtelenség a bolygók és a csillagok között nem volt semmilyen közeg, az egész tér vákum. Senki sem hitte el hogy a fény 150 millió km-t tesz meg a Naptól a Földig egy üres térben, senki sem hitte, hogy a fény terjedéséhez nincs szükség semmilyen közegre, és ezért kitaláltak egy feltételes hordozót amelyet 'luminioferous' (fény) éternek neveztek el. Ezaz elképzelés szerint, az éter mindenhol jelen volt ahol terjedtek a fény hullámok, és kitöltötte az egész kozmoszt amelyet eddig üresnek véltek.

Az éter ötlete mindenkinek logikusnak tűnt és az éter hamar elfogadott lett mint egy az anyagok között az űrben. Némely tudós elment egészen addig hogy megpróbálta kiszámolni az éter sûrûségét!

Michaelson - Morley kísérlete

Annak ellenére, hogy az étert nem sikerült kimutatni, senki sem kételkedett a létezésében. Mindenki úgy vélte, hogy érzékenyebb kísérletezésre van szükség. Ezt a kísérletet Michaelson és Morley gondolták ki és valósították meg 1881-ben.

A kísérlet amit Michaelson és Morley végeztek, egy nagyon egyszerű alapra, épült. Képzeljünk el egy versenyt két azonos repülőgép között. A két repülőgép egyszerre indul az A pontból. Az első repülőgép északra repül a B pontba majd visszatér az A pontba, míg a másik keletre száll a C pontba majd vissza az A-ba. Az A pont azonos távolságon van a B és a C ponttól, a távolság 800km. Mindkét repülőgép maximális sebessége 1600 km/h, ha nincs szél akkor könnyű kiszámolni, hogy egy óráig tart a verseny és döntetlen lesz.

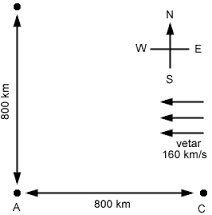
Ha figyelembe vesszük, hogy a szél keletről nyugatra fúj 160 km/h sebességgel, az ütközet nem végződhet győztes nélkül, mivel az első repülőgép lenne a nyertes. Azért győz az első repülőgép, mert a másik repülőgép széllel szemben szállna, így 1440 km/h sebességgel sebességgel haladna az egyik irányban, a maximum 1600 km/h helyett.

Ha kiszámolnánk mindkét repülőgép utazási idejét, azt az eredményt kapnánk, hogy az első repülőgép a versenyt 1 óra és 18 másodperc alatt teljesíti, a másik pedig 1óra 36 másodperc alatt.

Könnyen jutunk ahoz a következtetéshez, hogy abban az esetben, ha a szél iránya és a gyorsasága ismeretlen, ezek meghatározhatóak a verseny végeredményéből. Pontosan ezen az elven alapul Michaelson - Morley kísérlete. Két repülőgép helyett, ők versenyt "rendeztek" két fényhullám között, amelyek egymás között merőlegesek.

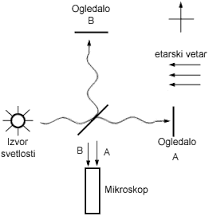
A berendezés amelyet használtunk ebben a kísérletben a képen bemutatott. A berendezés úgy van elhelyezve, hogy a Föld jobbra fordul, miközben érezni kellene az éter-szél "fújását".

A fényhullám a fény forrásától indul, ütközik a ferdén elhelyezett tükörrel, majd két, egyenlő erősségű hullámra osztódik. Az A hullám a síma A tükörig megy, míg a B hullám tükröződik és a B tükörig megy. Ez a két egyéni hullám megfelel a két repülőgépnek az előző példából. A hullámok, melyek tükröződnek az A és B tükörtől, visszautaznak, újra a ferde tükörhöz érkeznek és onnan pedig a hullám egy része a megfigyelő mikroszkópjához (interferométeréhez) érkezik. A megfigyelő ekkor regisztrálja mindkét hullámot a mikroszkópban és mindaz ami megmarad, már csak a "fotó-finish".

Ha két hullám érkezik az interferométerbe és ha az ő hullámvölgyei megeggyeznek, ők megnövekednek és a megfigyelő világosabb hullámot fog látni, mint amelyek egyénien. Az ilyen eredményt konstruktív interferenciának nevezzük. Ha valamelyik hullám némileg a másik előtt vagy után lenne a megfigyelő valamivel sötétebb hullámot látna a bejövőnél. Az ilyen eredményt részleges interferenciónak nevezzük. A harmadik lehetőség amely meg tud jelenni, a destruktív interferenció. Ez a fajta interferenció akkor keletkezik, ha a hullám dombjai eggyeznek a másik hullám dombjaival és akkor történik a hullámok közötti megsemmisülés.

Michaelson és Morley azt várták el, hogy az éter-szél az A és B hullámok eltéréséhez vezet, a megfigyelő pedig gyengébb intenzitású fényt kell, hogy lásson. Ők a kísérletet több alkalommal is elvégezték. Megismételték különböző nap- és évszakokban, de az eredmények mindig ugyanolyanok voltak- a hullámok egy időben érkeztek, az éter-szél pedig nem volt észrevehető.

A tudományban a helyzet igazán megzavartá vállt. Meg voltak győződve, hogy az éter létezik, de az összes próbálkozásuk a bebizonyítására hiábavaló volt. Sok kérdés vetődött fel, de kevés válaszra derült fény. Létezik-e az éter, vagy sem? Ha létezik, miért nem tudjuk detektálni? Ha pedig nem létezik, miért nem?

A ilyen tudományos körülményekben, amely telítve volt kedvetlenséggel és káosszal a megadott válasz egységes lett és elképzelhetetlennek tűnt első látomásra. A megoldás zsenialitást igényelt és ez Albert Einstein személyében és a megoldás javaslatában történt. Így jött létre a relativitás elmélete.

A speciális relativitáselmélet

A XX század kezdetén, Einstein relativitás elmélete sokkolta a világot. Előrelátta a klasszikus fizika szabályainak drasztikus változásait, melyek logikusak voltak, évszázadokig senki sem kételkedett a helyességükben.

Arisztotelész, Newton és az összes többi tudós Einstein előtt az abszolút időben hittek. Azt feltételezték, lehetséges lemérni a távolságot két esemény között, illetve, hogy az idő ugyanúgy tellik minden megfigyelőnek. Az idő teljesen független volt a tértől. Az emberek többségének ez teljesen normális volt. Az emberiség mégis meg kellett hogy változtassa a nézeteit a térrel és az idővel kapcsolatban. Még ha meg is változtatták, úgytűnik ezek a gondolatok összhangban vannak olyan dolgokkal, mint például az almák vagy a hegyek, de nem érvényesek már abban az esetben ha olyan dolgokról beszélünk amelyek a fénysebességet megközelítő sebességgel haladnak.

Einstein relativitás elmélete két fő részből áll: az 1905-ben megjelent speciális relativitáselmélet, és az 1916-ban megjelent Általános relativitás elmélete. Az speciális relativitáselmélet csak a tárgyakról és a rendszerekről (úgynevezett inerciális rendszereken) elmélkedik, melyek egyik a másikához, haladnak vagy állandó sebességgel haladnak vagy egyáltalán nem haladnak. Az Általános relativitás elmélet megfigyeli az olyan tárgyakat és rendszereket, melyek a másik tárgyhoz képest eltérő mozgást végeznek (neminerciális rendszerek).

A különleges elmélet feltételezései

Különféle kísérletek eredményei alapján Einstein két következtetésre jutott, két feltételezésre, melyeken alapszik a speciális relativitáselmélet.

Első feltételezés: minden fizikai törvény amely egységes egyenes vonalú mozgási rendszerben van, azonos alakban van kifejezve. Ez a feltételezés Einstein ugynevezett relativitás alapelve.

A feltételezés könnyebb megértéséhez, képzeljünk el egy egyszerű helyzetet amiben már biztos mindenki részt vett. Egy ember áll egy vonaton és lát egy másik vonatot a vele szemben lévő vágányban. Ha az egyik vonat elindulna, az ember könnyedén összezavarodhatna, hogy melyik vonat indult el. Természetesen, itt könnyedén megállapítható, hogy melyik vonat indult meg, csak rá kell nézni bármely tárgyra a sínek mellett. De most képzeljünk el egy űrhajón utazó utast a távoli jövőben. Induljon a Földről hozzávetőlegesen, állandó 8.000 km/h-ás sebességgel. Amíg ő a térben mozog és a Föld már látóterén kívül esik, és maga mögött figyeli a másik rakétát amely könnyen kerüli ki. A másik rakéta pilótája azt gondolja, hogy az első rakéta nem is mozog. Hogy bizonyítja be ez a csillag utazó, hogy mozog? Minden amit meg tud határozni, az a másik rakéta sebessége és semmi több. Ha a másik rakéta sebessége 1.600 km/h lett volna akkor több következtetésre juthatott volna:

• Az első utas 8.000 km/h sebességgel mozog a Földhöz viszonyítva, a másik pedig elhaladt mellette 1.600 km/h -val.
• A második utas mozdulatlan a Földhöz viszonyítva, az első rakéta pedig visszafelé halad 1.600 km/h-val.

Gyorsan arra a következtetésre lehet jutni, hogy egy mozdulatlan tárgy használata nélküli méréskor a megfigyelő nem tudja megállapítani, hogy ki mozog és ki áll, hogyha egyáltalán valaki áll. Tehát ha a megfigyelő távol helyezkedik el minden csillagtól és bolygótól, midenféle viszonyító pont nélkül melyet a sebesség méréséhez használna, soha sem fogja tudni megállapítani, hogy mozog-e vagy sem.

Ez a tény melyet Einstein feltételezett, hogy minden mozgás relatív. Soha sem lehet beszélni abszolút mozgásról, csak abban az esetben ha egy másik tárgyhoz viszonyított mozgásról beszélünk. Egyáltalán nem mondhatjuk azt, hogy ez a tárgy ezzel és ezzel a sebességgel mozog, viszont meg kell hagyni, hogy ezzel és ezzel a sebességgel mozog valamihez képest.

Második feltételezés miszerint a fénysebesség, illetve az interakció átvitelének maximális sebessége, azonos az összes tehetetlenségi rendszerben. Ez a feltételezés a Michaelson–Morley kísérlet következménye. Ez a kísérlet mutatott rá arra, hogy a fénysebességnek mindig ugyanannyi az értéke, függetlenül a fény terjedésének irányától.

Így egymagukban ezek a feltételezések igencsak érdekessek de, valami kapcsolat nélkül, köztük és a való világ között, illetve a megfelelő matematikai egyenletek nélkül melyek összekötnék az ötletet a valósággal, érdekessek lennének egy ideig de gyorsan feledésbe merülnének. Ezt a kapcsolatot a Lorentz-transzformáció egyenletei adták, ugyanis Lorenz előzőleg kifejlesztette ezeket a saját elmélete alapján. Ezek az egyenletek jól magyarázzák azok a kísérleti eredményeket melyek rávezették Einstent, hogy kételkedjen a Newton elméletek pontosságában. Ami még fontosabb, hogy ezek az egyenletek új előrelátásokat adtak, amelyeket a későbbiekben le lehetett ellenőrizni, és megbizonyosodni az elmélet pontosságában.

A Lorentz-transzformáció következményei különösek és meglepőek. A relativitás elmélet felfoghatatlannak hat, nem azért, mert nehéz megérteni az eredményeit, hanem azért, mert ezeket az eredmenyeket nehéz elhinni.

A hossz, a tömeg és a sebesség a speciális relativitáselméletében

A hossz kontrakciója

Amennyiben a megfigyelőnek az "A" rakétán lehetősége lenne lemérni a "B" rakéta hosszát, és ha egymás felé elindulnak "v" sebességgel, akkor az eredmény, amit a Lorenz transzformáció szerint az, hogy a "B" rakéta, mintha megrövidült volna, és a hosszát a következő képlet alapján van:

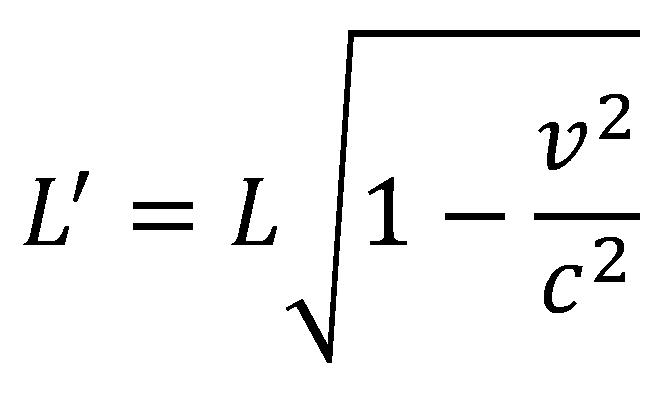
Ahol az "L'" az a hossz, melyet az "A" rakétáról meg lehetne mérni, "L" a valódi hossz, "v" a relatív sebességük, "c" pedig a fénysebesség.

A képen látható az összefüggés a rakéta hossza, amely nyugalmi állapotban 100 méter és a gyorsasága között a megfigyelőhöz viszonyítva. A grafikonon látszik, hogy a rakéta hosszúsága kétszer kisebb lesz 260.000 km/s sebességnél.

Ugyanez a képlet érvényes akkor is, amikor a megfigyelő a "B" rakétából méri az "A" rakéta hosszát. A következmény az, hogy nem tényező, hogy a rakéták távolodnak vagy közelednek. Az eredmény kizárólag a relatív gyorsaságuktól függ.

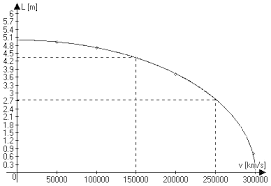
A hosszkontrakció hatását csak a fénysebességet megközelítő sebességeknél észlelhetőek. A kontrakció hatásának kimutatása lehetetlen, mivel a Földön ismert sebességek távol vannak a fénysebességtől. Ha például egy repülő 1200 km/h sebességgel indulna meg a megfigyelőhöz viszonyítva, kiszámolható, hogy a repülő egy centiméter milliódik részének a milliódik részével fog megrövidülni (nagyjából egy atommag nagyságával megegyező mennyiséggel). Természetesen ilyen apró rövidülést nem lehet észlelni.

A tömeg növekedése a sebességgel

A gyorsaság növekedésével nem csak a hosszúság változik. A megfigyelő sok más változást is észlel.

Feltételezzük, hogy az "A" és a "B" rakéta egyenlő tömeggel rendelkeznek amikor a Földön vannak és egymáshoz viszonyítva nyugalomban vannak. Mindkét rakéta tömege nagyjából 1000 kg. Ha a megfigyelő az "A" rakétából leméri a "B" rakéta tömegét amikor elindulnak, megfigyelhető hogy a "B" rakéta tömege megnövekedett és ezt a következő képlettel lehet kimutatni:

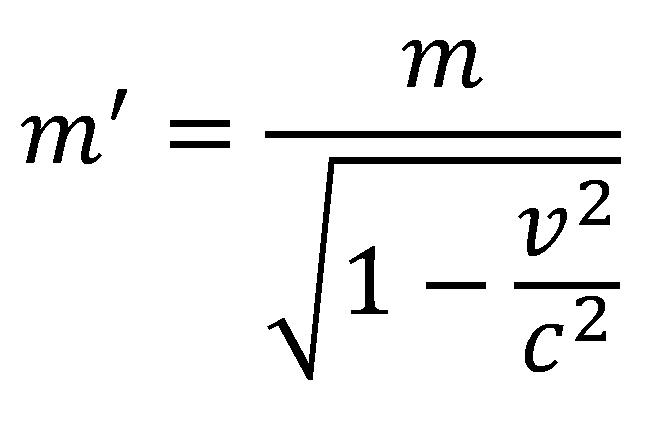
ahol m' az az érték, amelyet az A kap a B súlyáról, m a kezdetleges súlya a B-nek illetve ahogy másképpen nevezhető tömeg nyugalomban, v a relatív sebességük, a c pedig a fény sebessége. Az egyenlet alapján, arra a következtetésre lehet jutni, hogy ha az A és B rakéta tömege egyenként 1000kg, míg nyugalmi állapotban vannak a Földön, amenyiben a rakéták mozgásban lesznek relatív 150.000km/s sebességgel, az A rakétából úgy fog tűnni, mintha a B rakéta tömege 1200 kg lenne. A 260.000 km/s sebességnél a megfigyelő az A rakétából lemérheti, hogy a B rakéta 2.000 kg tömegű!

Természetesen nem kell figyelmen kívül hagyni, hogy a tömeg növekedése nem jelenti azt hogy a tárgy fizikai tulajdonságai (hossz, szélesség, magasság) is változtak sőt a tárgy még kissebb is lett.

Segességek összeadása

Feltételezve, hogy a megfigyelőhöz egyidejűleg közeledik egy vonat és egy autó, mindkettő 100km/h sebességel a megfigyelőhöz viszonyítva. Ezáltal ha a megfigyelő mérné a vonat és az autó sebességét, pontossan 100 km/h mérne. Ugyanígy ha a mozdonyvezető vagy az autó vezetője mérnék a saját sebességüket a megfigyelőhöz viszonyítva, ők is ugyanezt az eredményt kapnák. Viszont ha a mozdonyvezető mérné a saját sebességét az autóhoz viszonyítva, 200 km/h sebességet kapna, mivel a vonat és az autó is viszonylagosan a nem mozgó megfigyelőhöz, 100 km/h sebességel haladnak. Ugyanez érvényes az autó vezetőjére is, mivel ő is a vonathoz viszonyítva 200 km/h sebességgel halad. Az ilyen esetek igen gyakoriak a mindennapi életben és a következő egyenlet érvényes:

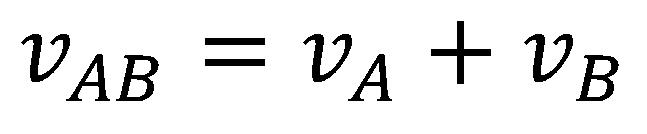
ahol a v_AB relatív sebesség, mellyel az A halad a B-hez viszonyítva (illetve a vonat sebessége az autóhoz viszonyítva, vagy fordítva), a v_a és v_b az A illetve a B sebességei a megfigyelőhöz viszonyítva.

Amennyiben a megfigyelő olyan helyzetben találná magát hogy a vonat helyett az A nevezetű űrhajót nézné amely fénysebességel haladna, a B autó helyett a B nevezetű űrhajót mely a fénysebesség felével haladna. Az űrhajók sebességeit meghatározni, a megfigyelő számára nem lenne nehéz feladat. Ugyanúgy a pilóták számára sem lenne nehéz feladat a sebességeiket meghatározni a megfigyelővel szemben. A gond ott kezdődik hogyha például a B pilóta kellene hogy meghatározza a sebességét az A pilótával szemben. Az előző logikával szemben a B hajó sebessége az A hajóval szemben 1,5c lenne, ami a második feltételezésel szemben lehetetlen. A speciális relativitáselméletben nem érvényes a hagyományos sebességösszeadás. Szükség vólt egy képletre mely összhangban lesz a követelményekkel meg a Lorenz transzformációkkal is. Az új szabály a relatív sebességek meghatározására a következő képlettel van kimutatva:

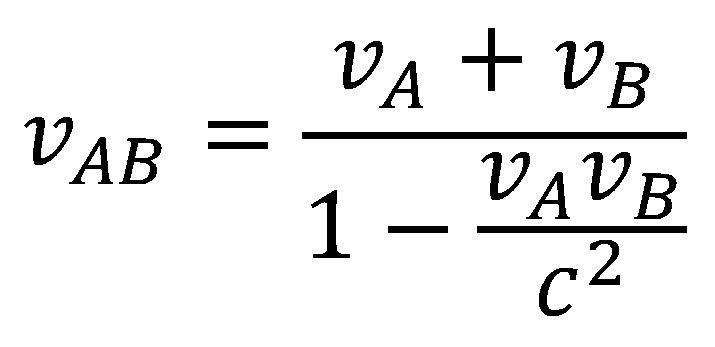
melyben a v_A és v_B a relatív sebességek melyekkel az A és a B halyók a mozdulatlan megfigyelővel szemben haladnak, a c a fénysebesség.

Minden gyakorlati alkalmazásnál a hagyományos sebességösszeadást pontosnak lehet elfogadni amennyiben a sebességek a fénysebességtől sokkal kisebbek. Amennyiben a sebességek megközelítik a fénysebességet az előző képletet kell alkalmazni.

A legnagyobb sebesség

A speciális relativitáselmélet öszes következménye közül a legfurcsább nagy bizonnyal az hogy semmi sem haladhat gyorsabban egy bizonyos sebességnél. A hossz változása képletéből látszik hogy a sebesség nővekedésével a hossz csökkenni fog amíg a sebesség el nem éri a fénysebességet, akkor a hossz egyenlő nullával.

Amennyiben feltételeznénk hogy a sebesség meghaladja a fénysebességet, a négyzetgyök alatt negatív szám lenne. A négyzetgyök a negatív számból imagináris szám, am azt jelenti hogy a hossz is imagináris szám lessz, illetve a tárgy nem fog létezni.

Hasonló eset történik a tömeggel is. A sebesség növekedésével a test tömege növekedik. Abban a pillanatban amikor elérné a fénysebességet a test tömege végtelenül nagy lenne.

Az elözőleg felsoroltak alapján egy következtetést lehet levonni - a fénysebesség a lehető legnagyobb sebesség. Semilyen test sem utazhat nagyobb sebességgel, mivel a hossza nullára csökken a tömege meg végtelenül nagy lessz. Pontosabb az állítás hogy egyik test sem mozoghat gyorsabban a fénynél, mivel a tömege végtelenül nagy lenne, a végtelenül nagy tömeg ilyen sebességű mozgásához végtelenül sok energiát kellene biztosítani.

A tömeg és az energia ekvivalenciája

A speciális relativitáselmélet legfontosabb jóslata az vólt hogy aránylag kis mennyiségű tömeg ekvivalens (egyenértékű) nagyon nagy energiamennyiséggel. Jól ismert hogy e jóslatnak a meggyőző bizonyítéka vólt az első atombomba robbantása Alamogordo (Új Mexicó Egyesült Államok) 1945 július 16-án.

A speciális relativitás elmélet előrelátja hogy a sebesség növekedésével növekszik a test tömege is, a következmény hogy a test energiája is nő. A nagyobb tömegű testnek az energiája nagyobb mint a kisebb tömegű testé ha ugyanazok a testek mozgási sebességei. Bizonyítható hogy a hozzáadott energia kapcsolatban van a hozzáadott tömeggel, méghozzá a hozzáadott tömeg beszorozva a fénysebesség négyzetével. Einstein ezek alapján következtetett arra hog a tömeg és az energia összefüggésben vannak, a kapcsolatuk a jólismert képlettel van megadva:

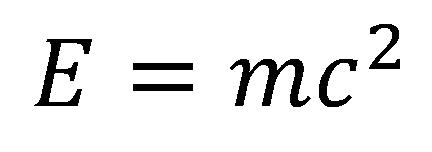
ahol az E az energia, m a test tümege a c a fénysebesség. Példaul, ha a képletbe egy kilógram szenet helyettesítenénk az energia 250 milliárd kilóvattóra lenne, illetve nagyságrendileg annyi enerrgia amennyit az összes erőmű egy hónap alatt termel az Egyesült Államokban. Egy kávéskanál szénpor elég lenne hogy a létező legnagyobb hajó többször is megtegye az utat Európa és New York között.

A mindennapi életből ismert tény hogy égés ideje alatt a szén sokkal kisebb energia mennyiséget fejleszt. Az szén égésénél felszabaduló energia vegyi folyamatok eredménye. Az atomok közötti kapcsolatok átrendeződnek de nem történik jelentős tömeg átváltozása energiává, mivel a szénből hamu, füst és korom lessz. Amennyiben ezeknek az anyagoknak (hamu, füst és korom) a súlyát megmérnénk a szén égése után az össz súly ugyanúgy 1 kg lenne.

Az idő a speciális relativitáselméletben

A speciális relativitáselmélet másféle gondolkodást ösztönzött a térrel kapcsolatban. Megmutatta hogy a hossz, tömeg és az energia nem állandóak hanem a sebességgel szűk kpcsolatban állnak. Meglehet hogy a relativitás különleges elmélenek a legnagyobb hozzájárulása az idő megértésével kapcsolatos.

Az idő viselkedése a speciális relativitáselméletben, ugyanazon a példán magyarázható mely ami idáig is használva vólt. Az A és B rakétákon az órák ugyanazt az időt mutatják amikor a rakéták egymás mellett vannak, például 12 óra. Ezt az időt nulladik időnek lehet nevezni.

Ahogy az idő múlik a távolság az A és a B rakéta között nő, mivel a rakéták egymáshoz viszonyítva relatívan haladnak, és egy idő intervallum után a távolság az A és a B rakéta között x lesz. A megfigyelő az A pontban megnézi a saját óráját és összehasonlitja a B pontban lévőnek az idejével, meg lesz lepődve hogy a két óra nem ugyanazt az időt fogja mutatni, a B pontbeli óra késik. Ez az helyzetet előrelátja a speciális relativitáselmélet, mivel az eredmények a következő képlet szerint fognak kinézni:

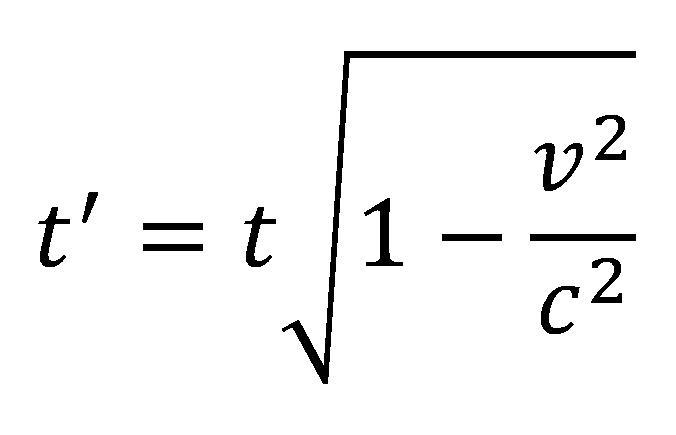
ahol a t' idő, amelyet az A megfigyelő lát a B órán, a t az idő melyet az A megfigyelő a saját óráján lát. Ahogy a relativ sebesség a növekszik, a B rakétán lévő óra lassabban és lassabban fog dolgozni, attól függetltnül hogy a rakéták közelednek vagy távolodnak egymástól.

Ezt az órák késési jelenséget a speciális relativitáselméletben időtágulásnak vagy időtágításnak hívják és akkor következik be amikor a két megfigyelő egyik a másik felé állandó sebességgel halad, mindkettőjüknek úgy tűnik hogy a másik órája késik.

Ebből a példából következtethető hogy az A és a B órák késése egymáshoz viszonyítva nem csak a fénysugarak viselkedésében van, hanem az ok a bizonyos időintervallum mely szükséges a fényhullámoknak is hogy elérjenek az egyik órától a másikhoz. Az idő tágulás hatása felelős egy teljesen másik nézetre az idővel kapcsolatban, amely régebben vólt elfogadva természetesnek. A relativitás különleges elmélete kidertitette hogy az idő eltér a nagy távolságokon lévő rendszerekben.

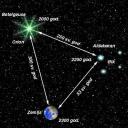
Amennyiben két megfigyelő, egyik a Földön a másik meg az Aldebaran közelében (a Taurus csillagképben), egy szupernóva robbanását figyelnék a Betelgeuse csillagon (az Orion csillagképben). A Föld és a Betelgeuse csillag között 300 fényév, a Betelgeuse és Aldebaran között 250 fényév, az Aldebaran és a Föld között 53 fényév a távolság.

Például a szupernóva robbanása 2000-ben történjen. A Földön a robbanás 300 év múlva lenne látható mivel akkora utat kell hogy megtegyen a fényhullám mely a robbanásról viszi az adatot a Földig. Másoldalról ugyanazt a robbanást Aldebaranon ugyanazt a robbanást 50 évvel előbb látnák mint a Földiek, mivel annyival közelebb vannak a robbanó csillaghoz.

Látszik hogy ez az esemény nem egyidejű a megfigyelőknek melyek három pontban vannak elhelyezve. A térbeli nagy távolságokon kívül lehetséges ezt a jelenséget kis távolságokon belül is észlelni amennyiben a megfigyelők sebességei megközelíti a fénysebességet.

Képzeljünk el egy utast aki a vonaton utazik, mely fénysebességhez megözelítő sebességgel halad. Az utas a kocsi közepén ül. A kocsi elején és hátulján ajtók vannak. Az ajtó nyitásával egyidejűleg az ajtó melletti lámpa kigyúllad. Egy adott pillanatban (a kocsiban ülő személy számára egyidőben), megnyílik mindkét ajtó. A megfigyelő aki nézi a vonatot nem fogja ezt az eseményt egyidejűnek látni, az ő szemszögéből elöször a neki közelebbi ajtó fog megnyílni (az a hátsó ajtó a menetirányhoz viszonyítva), utánna a távolabbi (a menetirányhoz viszonyítva). Ez a különbség onnan ered hogy az eső ajtó távolabb van a megfigyelőtől mint a hátsó ajtó és a fénynek nagyobb utat kell megtenni a megfigyelőig. Az események egyidejűsége vagy akár a sorrendje is csak a megfigyelő helyzetétől függ (a kocsi melyik fele van közelebb a megfigyelőhöz).

Szükséges említeni hogy minnél nagyobb a távolság a két egidejű esemény között, nagyobb lessz az idő is az események között ahogy majd a különböző megfigyelők fogják látni. Fordítva is érvényes, minnél kisebb a távolság a két "egyidejü" esemény között a megfigyelők számára is csökkennek az események közötti időintervallumok.

Ezen egyszerű példákon látszik hogy a régi Newton ötlet hogy az idő mindenhol ugyanaz, nem mindég érvényes. Ezenkívül az egyidejűség sem mindíg egyforma, látjuk hogy az eseményk sorrendje sem mindíg ugyanaz. A kérdésre hogy kinek a megfigyelők közül van igaza, a válasz: minjájuknak igazuk van!

Az ikrek paradoxona

Az idő tágulásának relativitás elméletéről pár igen érdekes és ijesztő ötlet született. Az idő tágulás hatásának érdekes felhasználási módjai lehetnek az ûrutazásban. Mindennek ami a fénysebességhez hasonló sebességel halad az az idő lelassul. Folyamatok mint például a biológia folyamatok, emésztés, atom aktivitás-minden késni fog!

Képzeljük el, hogy a "csillagközi utazó" vakációra tart az Arcturus csillagra, amely 33 fényévre van. Beszáll az ûrhajójába és belép egy utazásba, ami megközelitőleg fénysebességû. Ha folyamatosan ezzel a sebességgel haladunk, akkor valamivel több mint 33 évbe telik odaérni az Arcturusra, de Földi időben számolva, ha azonnal visszamennénk a Földre 66 évvel az elindulás napja után érnénk oda.

Ahogyan az ûrhajó hatalmas sebességgel halad a földhöz viszonyítva, minden mûvelet lelassul az ûrhajóban, az utasok nem fogják érezni, hogy 33 évig tart az út egy irányba az Arcturus légkörébe érnek körülbelül ebédidőre, és mire visszaérnek a Földre úgy fog tûnni, mintha csak egy nap telt volna el. Viszont ez a Földönélőknek 66 év elteltét jelenti, 66 évvel idősebbek lesznek.

Valami, ami bizonyítja, hogy a speciális relativitáselmélet összezavarodást és ellentmondást okozott a kezdetektől fogva. Ez az úgynevezett iker paradoxon vagy idő paradoxon.

Tételezzük fel, hogy a két iker közül az egyik elutazik egy távoli csillagra, majd vissza, míg a másik a Földön marad. Ez a csillag legyen mondjuk 4 fényévre a Földtől, az ûrhajó pedig fénysebességhez közeli sebességgel halad. Az egész út időtartama körülbelül 10 év lesz.

Ha összevetjük az idő múlásának arányát az úrhajóban utazó iker sebességével a Földön a képletből

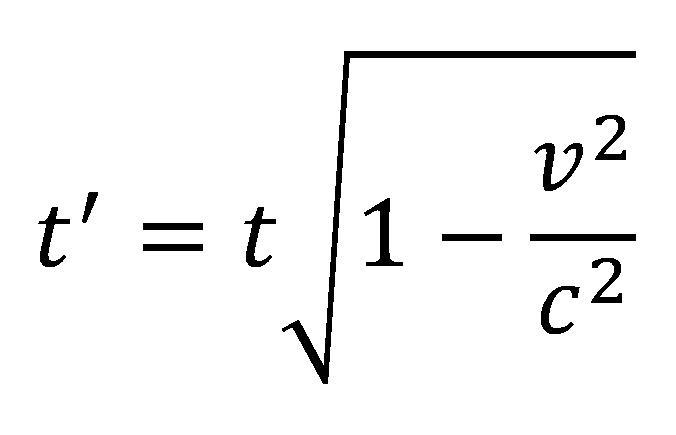
következik:

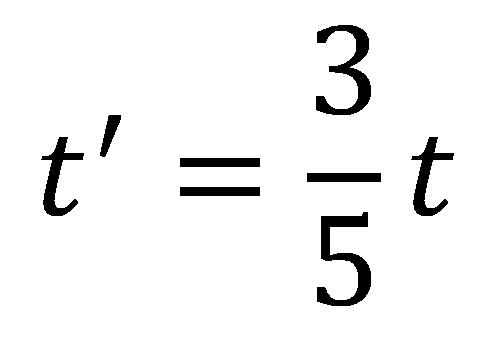
Ami azt jelenti, hogy habár az utazás 10 évbe tellett a Földi időszámítással, egy az ûrhajón levő óra szerint 6 évig tartott az út. Az utazásból visszatérve az egyik iker rájön, hogy ő nem öregedett annyit, mint a Földön maradt testvére.

A paradoxon úgy tûnik, ha minden relatív mozgást figyelembe veszünk, hogy a Föld az ûrhajóval ellenkező irányba haladt, majd visszatért míg az úrhajó lebegett. Ilyen feltételezések alapján minden mozgás ellenkező eredményt hoz az egyik iker az ûrhajón 10 évet vár hogy visszatérjen a testvéréhez míg valójában ez a Földön csak 6 évig tartott.

Nyilvánvaló hogy mind a két állitás igaz. Ez az az ellentét, ami miatt iker paradoxonnak nevezik.

A paradoxon megoldása nagyon egyszerű, illetve a paradoxon nem is létezik, mivel e két helyzet nem is szimetrikus, szóval matematikailag nem is reverzibilisek. A szimetria nemlétezése az hogy a rakéta az útján bizonyos gyorsulásokat végez az állítás hogy a Föld ment el útnak, nem pontos mivel ez esetben a Föld végezne gyorsulásokat a rakéta helyett ez meg közismert hogy téves feltételezés.

A speciális relativitáselmélet arra a következtetésre utal hogy az űrutas számára, függetlenül az idő mérésének módjától, kevesebb idő fog elmúlni mint a Földön lévők számára. Minden utas a Földre úgy tér vissza hogy kevesebb idő múlt el számára mint azoknak akik a Földön várják őket. Az idő lassulása a rakéta sebességétől és a megtett úttól függ.

Az ilyen következtetéshez vezet az összehasonlítás a fényjelek megfigyeléséből melyek a másik iker rendzeréből jönnek.

Az út első felében, a sebesség végett, melyel a rakéta távolodik a Földtől, a fénysugarak lassabban és csökkentett frekvenciával érkeznek a rakétához, mintamikor ugyanazon az adott helyen a rakéta nem mozogna. A fénysebesség 4/5 részével utazó rakéta esetéban a lassulás az úgynevezett relativisztikus Dopler hatás mely szerint a frekvencia 1/3 lessz a kezdetlegestől. Hasonló módon, visszatéréskor az iker a rakétában úgy látja az eseményeket a Földön, mintha háromszor gyorsabban történnének. Az utazás tejles ideje alatt a rakétában lévő iker a Földön történő eseményeket átlagban 5/3 (az 1/3 és a 3 átlaga) tempóban fogja észlelni. Ezekszerint a rakétán lévő iker az eseményeket a Földön gyorsítva fogja látni, mintahogy az események a rakétában történnek, a pontos arány 5/3 és a 1ö év a Földön olyan lessz mint 6 év a rakétában.

A helyzet melyet az iker a Földön lát fordított. Ő a fénysugarakat a rakétáról az út első felében kilenc évig fogja kapni. Az oka az hogy a rakétának öt év kell hogy a csillagig érjen és még négy év kell hogy a fénysugarak a Földig érkezzenek, mivela a távoli rakéta négy fényévre van a Földtől. Ez a kilenc év alatt a Földön lévő iker háromszor lassabban látja az eseményeket a normális tempótól, összhangban a relativisztikus Doppler hatásal.

Az eseményeket melyek a rakétán történnek útközben a Föld felé, a Földön lévő iker csak az utolsó tizedik évben fogja észlelni. Az utolső évben a Földön lévő iker az eseményeket a rakétán háromszoros sebességgel fogja látni. Az eredmény az hogy az eseményeket melyek a rakétán hat évig tartanak, a Fölfön lévő iker tíz éven át fogja észlelni, illetve átlagban a rakétán az idő lassabban fog folyni mint a Földön.

Innen látható miért aszimetrikus a helyzet az ikrek számára, és miért különböző az utazás ideje számukra. A rakétán lévő iker az útvonal felénél megfordul és az eseményeket a Földön gyorsítva kezdi látni, amíg a Földön lévő iker még négy évet kell hogy várjon hogy a rakéta fordulása utáni események kezdjenek érkezni hozzá, és utánna gyorsított ütemben történjenek. Illetve a Földön lévő iker az út ideje alatt hosszabb ideig kapja lassú tempóban az adatokat a rakétáról mint az iker a rakétában a Fölről jövő adatokat.

Úgy nézhet ki hogy a következtetések ilyen utazásról ellentétben vannak a speciális relativitáselmélettel hogy a fénysebesség a legnagyobb sebesség. Hogy lehet az hogy az utazás nyolc fényéves a rakéta meg hat év alatt teszi meg az utat amennyiben a rakétán van az utazás ideje mérve. Az egyszerű számítás (a megtett út elosztva az idővel) azt mutatja hogy a rakéta sebessége egy harmaddal nagyobb a fenysebességnél. Hol itt a hiba?

A sebesség "túllépésének" az oka az hogy a rakéta nem nyolc fényévnyi távolságot tesz meg. A távolság a csillagig a rakétán utazó iker számára le lessz rövidítve a Lorentz-FitzGerald rövidülés végett, és ez alapján a képlet alkalmazásával

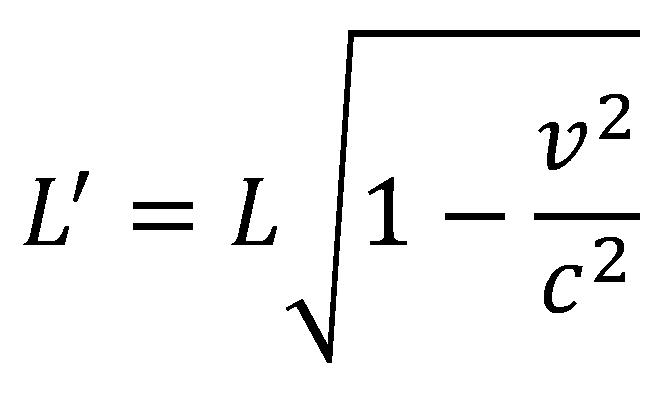
és a számértékek alapján a példából a rövidülés értéke 4,8 fényév az útvonalra visszafelé a Földre. Ezt az értéket elosztva az út idejével ami hat év, könnyen kiszámolható az átlagsebesség ami 4/5 fénysebesség.

Általános relativitáselmélet

Az Einstein speciális relativitáselmélet máar ismerős fogalom. Ez az elmélet jól magyarázza a fény "furcsa" viselkedését. Ez az elmélet segítségével Einstein megmagyarázta a Michaelson-Morley kísérlet eredményét, megmagyarázta hogy a fénysebesség miért ugyanolyan minden megfigyelő számára, függetlenül a megfigyelők elhelyezésétől és függetlenül hogy a mérés mikor lessz elvégezve. A testek viselkedése a fénysebességhöz közeli sebességeknél is meg lett magyarázva és miért is ez a legnagyobb lehetséges sebesség a természetben.

Függetlenül az összes magyarázattól amit ez az elmélet nyújt, egy új problémát is hozott magával. Ez az elmélet nem vólt összhangban a Newton törvényeivel, a hagyományos gravitációs törvénnyel. A Newton törvénye szerint minden test vonza a többi testet amely csak a test tömegétől és a testek közötti távolságtól függ. Ennél a hagyományos elméletnél a testek közötti interakció átvitele végtelenül nagy sebességgel történik. Ez az egyik alaptény a Newton-féle mechanikában és ellentétben van a speciális relativitáselmélettel, mely szerint semmi sem haladhat gyorsabban a fénysebességnél. Einstein többször is 1908 és 1915 között próbálkozott olyan elméletet felállítani amely "kibékítené" a két gravitációs elméletet. Ez 1915-ben sikerült Einsteinnek az általános relativitáselmélettel.

Az ekvivalencia elve

Az általános relativitáselmélet egy nagyon fontos és bónyolúlt elmélet, amely egy egyszerű következtetésen alapszik.

Jusson eszünkbeegy egyszerű helyzet - utazás liftel. Mindenki már észrevehette hogy amíg a liftel utaznak az utasok elveszítik az érzést a súlyról amit a kezükben tartanak. Például egy utas itazik a liftel egy bevásárlóközpont legfelső emeletéről a földszíntre. Ugyanakkor ez az utas bevásárlásból tér hazafelé es kezében nehéz bevásárlótáska van. Amíg a liftbe szál be, azon tanakszik mennyi mindent vásárolt és mennyi pénzt költött el. Becsukja az ajtót és a lift felfelé indul. Egyszerre az utas zavarba esik - kiszámolta hogy sok plnzt költött el, de a táska nagyon könnyű? Rövid idő múlva mégis a táska súlya olyan amilyennek kellene is hogy legyen. Megérkezik a földszíntre, beül az autójába, a lakásához érkezik beszáll a liftbe. A lift felfelé indul és... az utas észreveszi hogy a táska most sokkal nehezebb?

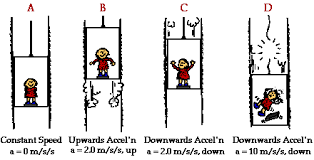
Ez az egyszerű példa alapján egyértelművé válik hogy a test súlya nem állandó hanem más tényezőktől is függ (itt említeni kell hogy ez esetben a súly erő, nem tömeg, mely két fogalmat a mindennapi életben sokan keverik), mint például a lift gyorsulása. Ez a test súlyváltozása a liftben nem szubjektív érzés, hanem valós fizikai jelenség. AMennyiben a liftben mérleg lenne amely a test súlyát mérné, a lift mozgása fügvényében, az eredmények eltérőek lennének: amikor a lift felfelé gyorsul a test súlya nagyobb lenne és fordított esetben a test súly kissebb lenne. Amennyiben a lift lefelé haladva annyira gyorsulna mit a szabadon eső tárgyak a mért súly a liftben nulla lenne, a súlytalanság állapota uralkodna. Amennyiben még jobban gyorsulna, a tárgyak a liftben "felragadnának" a lift menyezetére. Az esetekben amikor a lift nyugalmi állapotban van, vagy gyorsulás nélkül halad bármelyik irányban, ilyen jelenség nem észlelhető.

A test súlya az az erő amivel a Föld minden testet vonz, az az erő ami az előző példában jelenik meg, amíg a tömeg állandó marad. Einstein észrevette az összeföggést a gyorsulás és ez az erő között és forradalmi következtetésre jutott a tér egy pontjábanban a gravitáció effektusa és a gyorsulás ekvivalens és nem lehet őket megkülönböztetni. Ez a következtetés képviseli az ekvivalencia alapelvet.

Ez az elv alapján magyarázható az hogy utas súlyának a növekedése a liftben előidézhető gravitáció változtatásal is. Amennyiben az utas tudomása nélkül a lift át lenne költöztetve a holdra, az utas mennyire megijedne hogy könnyű a táskája közeben meg tudja hogy sok pénzt elköltott!

Önmagában az ekvivalencia alapelv egy egyszerű megfigyelésen alapszik de egymagában men vezethetett az egyik legfurcsább elmélethöz a XX században. Ahhoz hogy Einstein eljusson az általános relativitáselmélethez, alkalmaznia kellett egy akkoriban új matematikai eszközt, a tenzor számítást, melyet előzőleg Riemann fejlesztett ki. Ezek alapján Einstein három fontos következtetésre jutott, melyek a későbbiekben kísérletekkel be is lettek bizonyítva.

Einstein gravitációs elmélete

Az általános relativitáselmélet első feladata és az első ellenőrzése a bolygók Napkörüli pályáinak a magyarázata vólt. Sok éven át a Newton gravitációs elmélete elfogadható magyarázatot adot a bolygók pályáinak leírására. Az idő elteltével korszerűbbek lettek a műszerek és a megfigyelési technikák és bebizonyosodott hogy a hagyományos elmélet nem teljes pontossággal írja le ezt a jelenséget. A közismert tény az vólt hogy a bolygók Napkörüli pályákra kizárólag a gravitációs erő hat. Mivel az általános relativitáselmélet gravitációs elmélet ez vólt az első próbatétel számára.

A számítási eredmények melyeket az Einstein elmélete alapján jöttek létre megegyeztek a hagyományos elmélettel, egy nagy kivétellel. Az Einstein elmélete alapján a pályák térbelileg eltolódott elipszisek halmaza, illetve spirális (vagy rozetta útvonalat írnak időt is figyelembe véve).

A következő lépés az vólt hogy az eredményeket melyeket az általános reletivitáselmélet atott, le kellett ellenőrizni. A sebesség értéke mellyel az elipszisek kőröznek a Nap körül nagyon kis értékű, majdnem mérhetetlen. Az elmélet ellenőrzését nagy pontosságú mérésekkel lehetett bizonyítani. A legmegfelelőbb vólt annak a bolygónak a mérése mely leggyorsabb orbitális sebességel kőröz a Nap körül. Azon kívül olyan bolygónak kellett a megfigyelését végezni, melynek a pályája minnél jobban hosszúkás, hogy észrevehető legyen az orbitális sebesség ( többnyire a bolygók nagy része majdnem hogy szabályos körpályákon kőröz a Nap körül). Szerencsére egy bolygó pályája e két a feltételnek eleget tett, és ez vólt a Merkúr, amelynek a pályája sok fejfájást okozott a csillagászoknak. Már sok éve közismert vólt a tény hogy a Merkúr pályája minden 100 évben 574 másodpercel tolódik. A csillagászok 531 másodpercet a többi bolygó gravitációs hatásával tudtak megmagyarázni. A megmaradt 43 másodpercre nem vólt magyarázat. Vóltak próbálkozások ezt a különbözetet egy még felfedezetlen bolygó hatásának hozzárendelni de ilyne bolygót nem lehetett észlelni.

Az általános relativitáselmélet megjelenéséig a Merkúr pályáját nem lehetett megmagyarázni. A relativitáselmélet pontos értéket adott, mely megegyezett a megfigyelésekkel és a mérésekkel. Ez vólt az első sikere az általános relativitáselméletnek.

A tér-idő görbület jelentősége

Az előző mondatok alapján tévesen lehet következtetni hogy a hagyományos elmélet és az általános relativitáselmélet között nem nagy a különbség. A különbség nem a számtani eredményekben van hanem a lényegben, melyeken alapoznak, a gravitáció leírásában. A Newton a gravitációt egy egyszerű erőként értelmezi, amíg az általános relativitáselmélet szerint a gravitáció a tér-idő egy tulajdonsága. Az általános relativitáselmélet szerint a gravitáció annak az eredménye, hogy a tér-idő görbül a benne elhelyezett tömegek és energiák végett. Valahol távol a világűrben, távol minden nagytestű objektumtól a tér-idő teljesen síma. Közeledve bármilyen nagytestű objektumhoz a tér-idő sík görbülete nől. A gravitációtér ereje a tér-idő görbületének a mértéke.

Ilyen leírás alapján a tér-időben a bolygók egyenes útvonalakon haladnak és az útvonalai nekünk görbéknek tűnnek a tér-idő görbülete miatt. Az útvonalak melyeken a testek ebben a görbült tér-időben haladnak geodéziai vonalaknak nevezik. A geodéziai vonalak a legrövidebb vonalak melyek a két tetszőleges pont közötti legrövidebb távolságot írják le. Nézzük a Föld felületét mint egy görbült kétdimenziós teret. Amennyiben a földgömbön két várost kötnénk össze a legrövidebb útvonallal észlelnénk hogy ez nem egyenes vonal hanem görbe vonal. Utánna repülőbe ülnénk és követnénk az útvonalat amit lerajzoltunk. Úgy tűnne hogy egyenes vonalon haladunk és a he nem tudnánk hogy a Föld kerek nehezen győzne meg bennünket bárki is hogy nem egyenes hanem görbe pályán haladunk. Hasonló az eset a négydimenziós tér-idővel is.

Az általános relativitáselmélet azt mutatja hogy az anyag közli a tér-időnek hogy görbüljön a görbített tér-idő meg közli az anyaggal hogy viselkedjen.

Ez vólt még egy furcsa és első látomásra teljesen elfogathatlan ötlet melyet az Einstein relativitáselmélet adott. Ritka vólt az aki elhitte ezt, és Einstein ajánlotta hogyan lehet a feltételezést ellenőrizni hogy mi valójában négydimenziós görbült tér-időben élünk.

A kísérlet melyet Einstein ajánlott azon alapozott hogy a fénysugár mely egy távoli bolygóról érkezik felénk, a Nap mellett haladva nem egyenes útvonalon érkezik, hanem ívet fog leírni.

Az ilyen mérés végrehajtásához szükség vólt hogy a csillagászok megmérjék a fénysugár súlyát a Napon. Mint minden tárgynak úgy a fénysugárnak is megvan a súlya. A fénysugár sok részecskéből áll, melyeknek foton a nevük és amíg mozgásban vannak, bizonyos súlyuk is van. Mindenki számára valószínű hogyan lehet bármelyik testnek a súlyát megmérni: megvárjuk amíg leesnek és rátesszük őket a mérlegre. A fotonokkal nem ilyen könnyű az eset. Lehetetlen őket megfogni és rátenni a mérlegre, mivel a fotonoknak mincs tömege amikor nem mozognak, ők csak mozgás ideje alatt léteznek. Elméletileg nézve a fotonok tömegének mérése egyszerű - amennyiben a gravitáció kihatásal van a fénysugárra a fotonok nem fognak egyenes útvonalon haladni, a sugár ívelni fog. AMennyiben a gravitáció nincs kihatásal a fénysugárra a fénysugár egyenes útvonalon fog haladni. Ilyen módon lehet megállapítani a tér mértanát. A mérés végrehajtásához a fénysugár egy nagy testű és erős gravitációval rendelkező tárgy kőzelében kellene hogy elhaladjon a legalkalmasabb test ilyen mérésre a Nap vólt.

A fénysugár egy távoli csillagtól kell hogy jőjjön. Akkor amikor a Föld és a csillag között nincsennek nagy testű tárgyak a fénysugár a Földre egyenes útvonalon fog érkezni. A szükséges pont az amikor a távoli csillag fénye közvetlen a Nap mellet elhaladva érkezik a Földre.

Itt jelentkezett az a gond hogy a Nap fénye miatt lehetetlen bármilyen csillagot látni. A megoldást Einstein ajánlotta hogy a mérés a teljes napfogyatkozáskór legyen.

A folyamat során a csillagot le kellett fényképezni amikor a Nap nem vólt jelen és ugyanazt megismételni amikor teljes napfogyatkozás van. A képeken hogyha az általános relativitáselmélet pontos a csillagoknak a helyzete Nap környékén eltérő kellene hogy legyen az első képhez viszonyítva. Einstein kiszámolta hogy a csillag látszólagos eltérése 1,74 ív-másodperc kellene hogy legyen.

A legmegfelelőbb napfogyatkozás 1919 május 29-én vólt. Különösen megfelelő helyzet még az is vólt hogy az év május végére sok fényes csillag vólt jó irányban és könnyű vól közöttük egyek kiválasztani. E nagy feladatra két Brit csapat készült fel. Az egyiket A.C.Cromlin vezette és ők észak Brazilba utaztak. A másik csapatot A.S.Edington vezette és ők egy szigetre utaztak a Guineai öbölbe. A teljes napfogyatkozás ideje alatt nagy mennyiségű kép lett készítve melyek Britanniába lettek szállítva és részletesen elemezve.

Az első csapat fényképei alapján a csillag elmozdulása 1,98 ív-fok vólt a második csapat képei alapján meg 1,6 ív-fok vólt. Az ilyen jó összhang az elmélet és a kísérlettel kapott értékek jól bizonyították az általános relativitáselmélet pontosságát.

A több mint hat évtizeden át ismétlődő ilyen és hasonló kísérletek nem hoztak oylan eredményeket melyek megkérdőjelezték vólna az általános relativitáselméletet.

A gravitáció és az idő

Már említve lett hogy a Relativitás elmélet nem tesz különbséget a tér és az idő között. Idáig láthatóak voltak az átalános elmélet következményei a tér "kinézetére". Hasonló következmények léteznek az idő múlásánál is.

Az általános relativitáselmélet előrelátja hogy a gravitáció lassítja az időt. Csak nagyon messze a tér-időben, távol bármilyen gravitációs terektől, ott ahol a tér-idő teljesen síma az órák rendes ütemmel dolgoznak. Bármilyen nagyobb testhez közeledve az idő múlása lassul. Ez alapján a következmény az hogy a földön valamivel gyorsabban fog múlni az idő mint Jupiteren. A Jupiteren az idő valamivel gyorsabban fog múlni mint a Napon. Einstein kiszámolta hogy egy másodperc a Földön 1,000002 másodperc a Napon.

Több próbálkozás vólt e különbség mérésére, egyik próbálkozás sem lett sikeres. Az első kísérlet mely bizonyította ezt az általános relativitáselmélet állítását, a földön lett végrehajtva 196ö-ban, öt évvel az Einstin halála után. A Hardvardi egyetemen dr Robert Paund és aszisztense Glenn Rebka kísérlete bebizonyította hogy a Földön és a kisebb magasságokon a Föld felszíne felett nem egyformán múlik az idő. Ők egy 22,6 méteres tornyot használtak. Az egyik óra a Földön vólt a második meg a torony tetején. Az ilyen pontos mérésre szükség vólt nagyon nagy pontosságú időmérő eszközökre. A természetben nagyon nehéz pontosabb időmérő eszközt találni mint az atomóra. A kísérletben az időmérő eszközök a rádioaktív Co-57 magjai vóltak. Az időmérő eszközök felszerelése után detektorokkal kellet a gamma sugár foton frekvenciáját mérni melyek a rádioaktív bomlásban tűntek el. Az eredmények nagyon jól eggyeztek meg az Einstein elmélete által előrelátott értékekkel.

Öt évvel a teremtőének halála után, az Einstein elmélete gyakorlatban is be lett bizonyítva. Nem vólt több kétely, az emberiség megkapta a gravitáció legjobb elméletét. Ez az elmélet pontossága bizonyítása után nem csökkentette az érdeklődést iránta, ellenkezőleg még érdekessebbé vált és új nézeteket nyitott.

Fizika vagy tudományos fantasztika

Sokan biztosan már feltették maguknak azt a kérdést hogy valyon miért olyan nagy a relativitáselmélet jelentősége. Jól ismert tény hogy a mindennapi életben a "régimódi" Newton magyarázata a gravitációról mint egy erőről tejlesen hibátlan. Az emeberek küldése a Holdra, az űrhajók küldése más bolygókra, tejlesen összhangban van a Newton elméletével. Akkor miért kell bónyolúlt számításokkal a relativitáselmélet alapján vesztegetni az időt, amikor minden ismert helyzetben a Newton elmélete elfogadható eredményeket ad?

Sokáig a Relativitáselmélet megjelenése után senki sem hitt abban hogy az Univezumban létezik olyan hely ahol a Newton törvényei nem érvényesek, a hely ahol a tér és az idő annyira elgörbült hogy szükséges az általános relativitáselméletet alkalmazni. A Föld, Nap, Jupiter és más ismert égitestek közelében a grvitáció olyan gyenge hogy a téridő görbülése nem jelentős és a Newton törvényei jó eredményeket adnak.

A XX évszázad hatvanas éveiben a fizikusok rájöttek a csillagok életútjára a születésüktől a halálukig. Egyes életfázisában a csillagok melyeknek a tömege sokkal nagyobb mint a mi Napunké a Newton törvényei nem "működnek". Egy ilyen nagy tömegű élete végén a gravitáció évek milliói után legyőzi a csillag belső erejeit (hősugárzás, elektrosztatikus taszítás). Akkor a csillag zsugorodni kezd, a sűrűsége és a gravitációja nővekszik (a gravitációs erő fordított arányban van a távolság négyzetével, ami azt jelenti hogy ha a csillag felére zsugorodik, a gravitációs ereje négyszerezedik, közben a tömeg változatlan). Ahogy a gravitáció növekszik a tér-idő jobban görbül. Ez a folyamat eleinte lassú, egy pillanatban, hirtelen a gravitáció legyőzi a haldokló csillag részecskéinek az erejeit. Másodpercek alatt a csillag zsugorodik és a részecskéi (protonok, neutronok és elektronok) egymásba olvadnak. Többé a természetben nincs olyan erő amely ezt a gravitációs erőt legyőzné, a csillag el van ítélve hogy fekete lyuk legyen.

Ahogy a csillag közeledik a sorsa vége felé a csökken a fény is amely el tudja hagyni a csillag gravitációját. A tér-idő görbület már akkora hogy csak a függőleges sugarak tudják elhagyni a csillagt. Amennyiben valaki biztonságos távolságból tudná követni ezt a folyamatot, őgy látná hogy a csillag fénye csökken.

Végleg az egyik pillanatban a görbület akkora lessz hogy a fény nem tudja elhagyni a csillagot. Ez akkor történik amikor az első kozmikus sebesség nagyobb mint a fénysebesség, amely a legnagyobb a természetben. Ilyenkor azt mondják hogy a csillag beleesett a saját eseményhorizontjába. Az "eseményhorizont" kifejezés nagyon megfelelő. Ez szószoros értelemben sík a tér-idő mértanban amely mögött nem lehet látni egy eseményt sem. Nincs lehetőség arra hogy létható legyen bármi is ami az eseményhorizontban történik. Az olyan hely ami nem a mi tér-időnkben van, az már nem a mi világegyetemünkben van.

A csillag szerencsétlenségére a gravitáció nem áll meg csak azon hogy a csillagot összetömörítette a eseményhorizontba. A gravitáció addig növekszik amíg az egész csillag egy pontba lessz tömörítve. Abban a pontban a nyomás és a sűrűség végtelenül nagy, ami még fontosabb a tér-idő görbülete végtelen. Az az út melyen felé minden csillag halad. Minden atom és minden részecske teljesen össze van morzsolva azon a helyen. Az a fekete lyuk központja, más néven szingularitás

A fekete lyuk üres a struktúrája egyszerű. A fekete lyuknak csak két része van: Szingularitás és az eseményhorizont. Itt semmi sem létezik. Nincs atom, semilyen szikla, gáz vagy por. Semmi! Az öszes csillaganyag össze van morzsolva és a fekete lyuk középpontjába tömörítve a szingularitásba.

Az Általános relativitáselmélet sok furcsa effektuma mely elhanyagolható a Földön vagy a Nap közelében, sokszorosan nagyobb a fekete lyuk közelében. Az idő lassulása a Földön elhanyagolható, de az eseményhorizontban amely kőrbeveszi a fekete lyukat az idő teljesen megáll. A mindennapi tapasztalatunk szerint mi a térbe három irányban mozgunk: le-föl, jobbra-balra, előre-hátra, amíg az időben csak egy irányban tudink haladni: a múlttól a jövő felé. Ezzel ellentétben a fekete lyukban meg van a mozgás szabadsága az időben, de a szabadság az időben magával hozza azt hogy a térben nem lehet mozogni. A fekete lyukban minden út előbb-utóbb a szingularitásba vezet.

A fekete lyukak a legegyszerűbb objektumok a világűrben, ugyanakkor a legfurcsábbak is.

Képzeljünk el egy nagy tömegű csillagot az élete végén. A tér-idő az összeomlás előtt csak valamennyire görbült. Ahogy a csillag tömörödik, a ter-idő görbülete nől (a tér-idő síkban növekszik a mélyedés). Azt hogy mi történik a "mélyedésel" Einstein és Rozen analizálták a XX évszázad harmincas éveiben. A meglepetésükre rájöttek hogy a "mélyedés" másik oldala megnyílik és összeköt egy másik világűrrel! A fekete lyuk e furcsa tulajdonsága Einstein-Rozen hídnak lett elnevezve. A későbbiekben arra a következtetésre jöttek hogy az Einstein-Rozen híd összeköthet két pontot a tér-időben a mi világűrünkben is. Az ilyen alagutakat másnéven "féreglyukaknak" is neveznek.

Érdekes említeni hogy a féreglyukak összeköthetik a mi világűrünket saját magával sok helyen, és ezek a helyek különböző pontok lehetnek a tér-időben. Másszóval belépésel egy ilyen "más világűrbe", újból be lehetne lépni a mi világűrünkbe. Ezt időgépnek is lehet nevezni. Elméletileg be lehetne sűlyedni egy forgó féreglyukba és óvatosan irányítva az űrhajót megjelenni a mi világűrünkben a Földön milliárd évvel ezelőtt amikor a bolygónkon a dinoszauruszok jelentek meg.

Szép lenne egy ilyen időgépet használni. Sok érdekes eseményt lehetne meglátogatni a múltban, megtekinteni, vagy esetleg részt is venni. Az ilyen időgép fizika vagy tudományos fantasztika, az olvasó döntse el...

* - * - *

Az utolsó huszonöt évét Einstein az egységées mező elméletének szentelte, egy elmélet mely leírná az elektromos, mágneses és gravitációs mezőt. Ő 1953-ban, két évvel halála előtt, nyilvánosságra hozta kutatása eredményeit melyek az egységes mező elméletére vonatkoztak. Úgy gondolta hogy sikerült egységesíteni a gravitációs és elektromágneses jelenségeket egy egységes elméletbe. Az egyenlet halmazok melyek az elméletéből származtak végtelenül sok megoldást adtak és nincs lehetőség meghatározni a pontos megoldást közöttük, meyl erre a világűrre érvényes. Az hogy ez az Einstein elmélete pontos-e vagy nem, még senki sem tudja.