4. osztály - Fizika

A részecskék kettőssége

A duális hullám-részecske természet nem csak a fénynél (illetve elektromágneses hullámoknál) jelentkezik. A korszerű fizika szerint a dualitás általános tulajdonság az objetumnak a mikrovilágban, illetve molekulák, atomok és más apró részecske. A kvantum mechanikában még a makrovilágbeli testek tulajsdonságai (például kristályok) mint ilyen részecskék tömege a duális természetükkel van magyarázva.

De Broglie hipotézis

Minden részecskéhez mely v sebességgel halad és p lendülete van, hozzárendelhető egy hullám, melynek a hullámhossza:

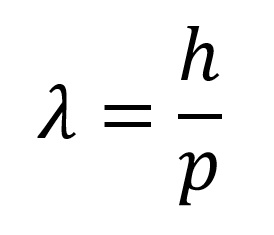
Az előző képletet de Broglie összefüggésnek nevezik. A hullám ami a részecskéhez van hozzárendelve de Broglie hullám a hullámhossz meg de Broglie hullámhossz. A de Broglie összefüggés érvényes a relativisztikus és a nemrelativisztikus részecskékre is. Az előző képletet ilyen formában is lehet írni:

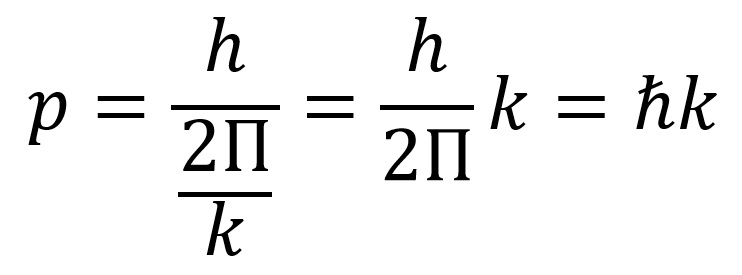
Ahonnan a de Broglie hullámának a hullámvektora:

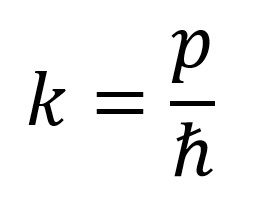
Ahol a p a részecske lendülete. Amikor a részecske valami erőtérben halad (potenciális mező), abban az esetben a teljes energiája:

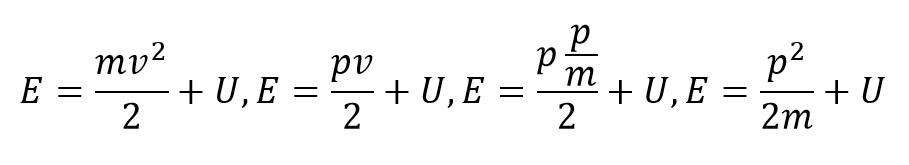
A részecske amely valami erőtérben található, nemszabad részecske, ellenkezőleg a részecske mely erőtéren kívül található szabadrészecskének nevezhető. Amennyiben a mozgási energia a lendület alapján van kifejezve és a és a helyzeti energia U-val van jelölve, a nemszabad nemrelativisztikus részecske teljes eneriája:

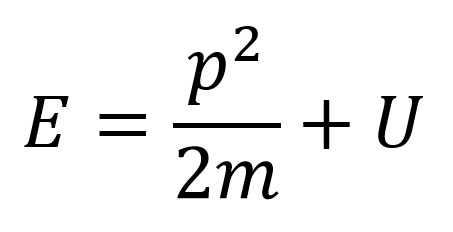
Az előző képlet és a de Broglie összefüggése alapján levezetni a képletet a hullámhosszra mely hozzá van rendelve a nemszabad nemrelativisztikus részecskéhez.

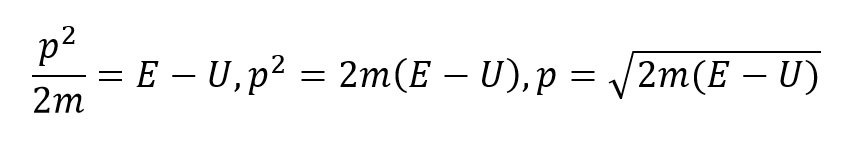
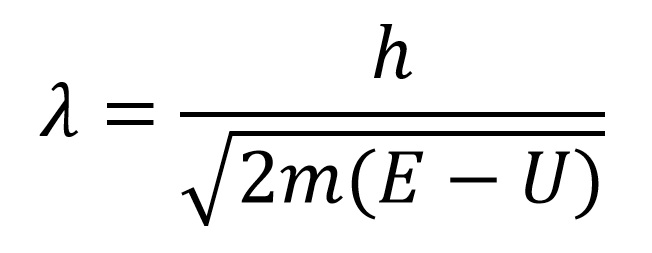
Amennyiben a részecske szabad akkor a helyzeti energiája nulla, és a szabadrészecske de Broglie hullámhossza:

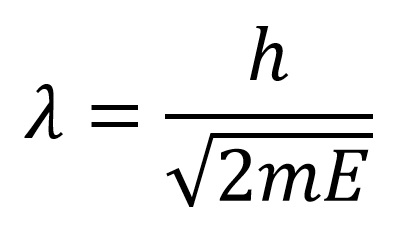
Ahol az E a részecske teljes energiája mely megegyezik a mozgáseneriával. Ezek szerint amennyiben a szabadrészecske gyorsabban mozog a kinetikus energiája nagyobb a de Broglie hullámhossza meg kisebb.

Amennyiben léteznek a de Broglie hullámok akkor észlelni lehet a diffrakciójukat is. A diffrakciójukat diffrakciós ráccsal lehet észlelni azzal a feltétellel mely szerint a rács állandó nagyságrendje a megegyezik a hullámhossz nagyságrendjével mely a diffrakciós képet fogja alkotni. Emiatt szükséges a de Broglie hullámhossz meghatározása.

Az elektronok diffrakciója

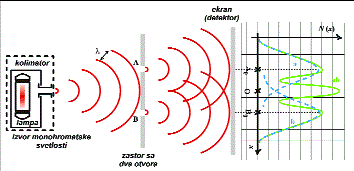
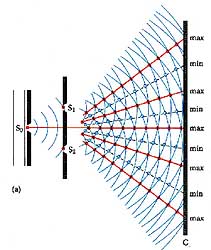
A diffrakció egy fizikai jelenség, mely főleg a hullámoptikában fordul elő, lényegében a hullámok elhajlását értjük alatta.

A Huygens-elv értelmében egy hullámfelület minden pontja elemi hullámok kiindulópontja is egyben. Ugyanakkor a Huygens–Fresnel-elv kimondja, hogy a hullámtérben megfigyelhető hatást az adott hullámfelületből kiinduló koherens elemi hullámok interferenciája határozza meg. Ha a hullámok útjába a hullámhosszhoz képest viszonylag nagy méretű réssel ellátott akadályt teszünk, akkor a nyíláson áthaladó hullámok közelítőleg egyenesen haladnak tovább. Ha azonban a rést elegendően kicsire szűkítjük, a hullámok behatolnak abba a térbe is, ami eredetileg az akadály által árnyékolva van – ilyenkor tapasztalható az elhajlás, azaz a diffrakció.

Az elektronmikroszkóp

Az elektronmikroszkóp egy olyan mikroszkóp, ami elektronnyalábot – nagy sebességre felgyorsított elektronokat – használ a megfigyelendő tárgy leképezésére. A hagyományos fénymikroszkópéhoz képest sokkal jobb felbontása révén az elektronmikroszkópos felvételeken a sejten belüli részletek, de atomok kontúrjai, szabályos kristályrácsszerkezet körvonalai is megfigyelhetők.

Mivel az elektron hullámhossza sokkal rövidebb a látható fény fotonjáétól, az elektronmikroszkóp felbontási határa is sokkal kisebb mint a hagyományos fénymikroszópé: 0,1 - 0,2 nm az elektronmikroszkópnál illetve 200 - 350 nm a fénymikroszópnál.

A mikroszkópok összehasonlítása:

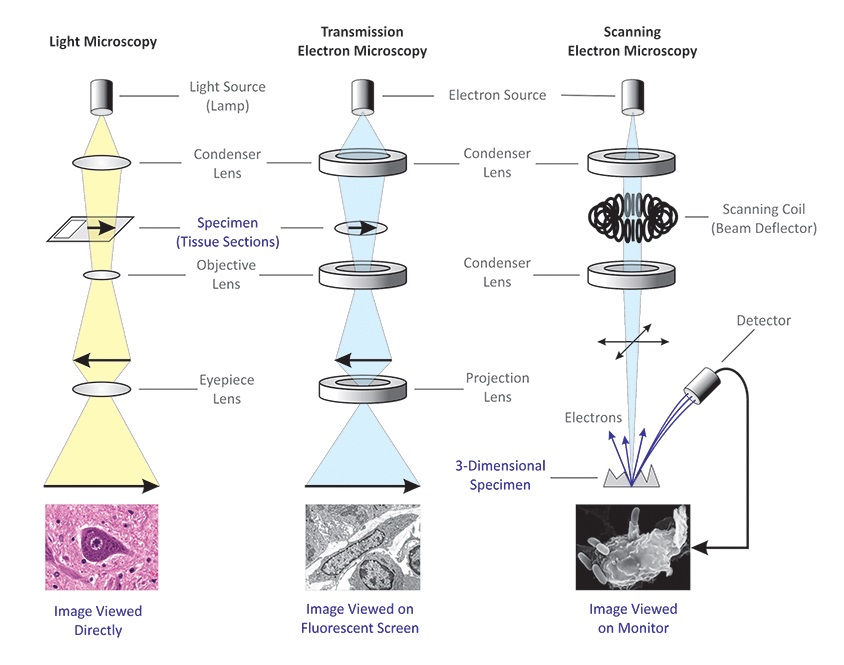
Az elektronmikroszkóp működési elve:

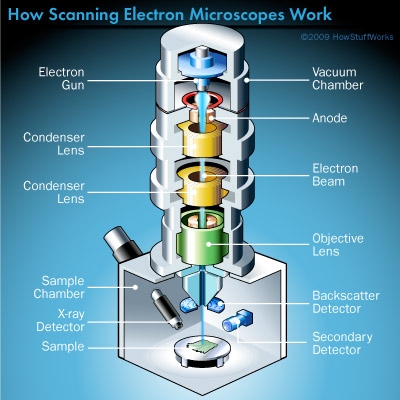
Emberi haj:

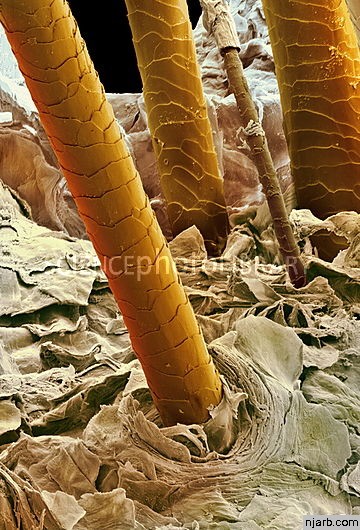
Vörös vérsejtek:

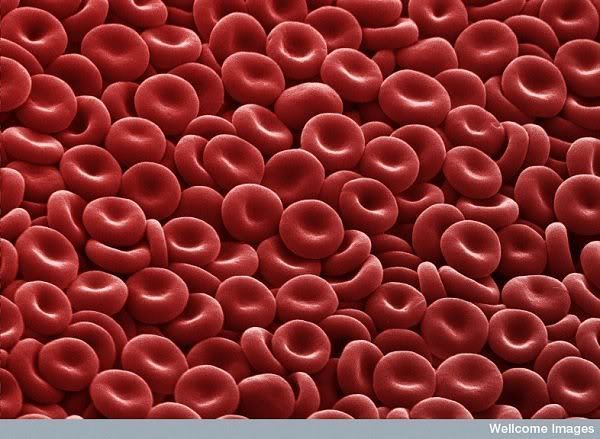
Heisneberg-féle határozatlansági reláció

A kvantummechanikai határozatlansági reláció (németesen: összefüggés, angolosan: elv) alapvető, elméleti határ bizonyos fizikai mennyiségek egyszerre, teljes pontossággal való megismerhetőségére. Ilyen mennyiségpár például a hely és az impulzus, minél pontosabb értéke van az egyiknek, annál pontatlanabb a másiknak. Az eredeti heurisztikus érvelést, hogy léteznie kell egy ilyen határnak, Werner Heisenberg adta 1927-ben, aki után gyakran Heisenberg-féle relációnak is szokták nevezni. Egy formálisabb megfogalmazást adott Earle Hesse Kennard (és tőle függetlenül egy évvel később Hermann Weyl), ami a helyzet és az lendület mért értékeinek szórásait kapcsolja össze:

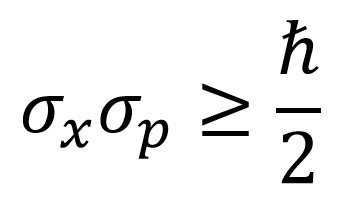
ahol ℏ Dirac állandó, illetve a redukált Planck állandó.

Schrődinger egyenlet

A de Broglie hullámok statisztikus magyarázása és a Heisenberg határozatlansági reláció kimutatták, hogy a kvantummechanikai egyenlet, mely leírja a részecskéket a mezőben kell, hogy egyidejűleg leírja a részecskék hullámtermészetét is. Ezek szerint az egyenlet alapja a hullámfüggvény kell, hogy legyen Ψ(x, y, z, t) vagy az |Ψ|² érték. Mivel a keresett egyenlet figyelembe kell, hogy vegye a részecskék hullámtulajdonságait, az egyenlet hullámegyenlet kell, hogy legyen, mely hasonlít az egyenletre, mely az elektromágneses hullámokat írja le.

A nemrelativisztikus kvantummechanika egyenletét 1925.-ben megfogalmazta és 1926.-ban nyilvánosságra hozta Ervin Schrődinger, Osztrák fizikus. Mint minden fizikai alapegyenletet (Newton egyenlete hagyományos mechanikában, Maxwell egyenlete az elektromágneses mezőkre), a Schrődinger egyenletét nem vezetik le, a kísérletek eredményei bizonyítják a pontosságát.

A Schrődinger egyenletét a következőképpen lehet leírni:

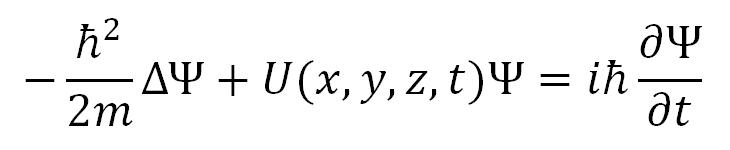
ahol az m a részecske tömege, Δ Laplace operátor (ΔΨ = ∂²Ψ/∂x² + ∂²Ψ/∂y² + ∂²Ψ/∂z²), az i az imagináris egység az U(x, y, z, t) a részecske helyzeti energiája a mezőben, melyben mozog. Mivel nemrelativisztikus Schrődinger egyenletről van szó, ez egyenlet érvényes bármely részecskére, mely sebessége v sokkal kisebb a fénysebességnél c (v << c).

Ez az egyenlet Schrődinger egyenletének időfüggő általános formája és számtani szemszögből másodfokú parciális differenciális egyenlet.

A mikrovilágban több helyzetben ezt az egenletét egyszerűsíteni lehet. Az egyszerűsítés abból áll, hogy a Ψ hullámfüggvényt időfüggetlennek lehet tekinteni. Ez lehetséges amennyiben a mező, melyben a részecske található, stacionáris, illetve a függvény U = U(x, y, z) időfüggetlen, és potenciális energiatermészete van. Ilyen módon a következő egyenletet lehet felírni:

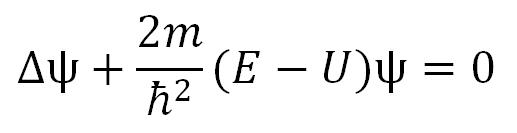
mely a Schrődinger egyenlete stacionáris mezőre, egyszerűen Schrődinger egyenletnek nevezik.

Az egyenletben az E paraméter a részecske összenergiáját képviseli. A differenciálegyenletek elméletében ki van mutatva, hogy az egyenletnek megoldásai csakis egyes E értékekeire léteznek. Ezeket az értékeket sajátlagos értékeknek nevezik. A Schrődinger egyenlet megoldásai, melyek megfelelnek a sajátlagos értékeknek sajátlagos függvényeknek nevezik. A sajátlagos értékek kontinuálisak és diszkrétek is lehetnek. Az első esetben folyamatos illetve kontinuális spektrumról van szó, a második esetben diszkrét illetve vonalspektrumról van szó.

Az egydimenziós esetben, amennnyiben az U(x), mező, melyben a részecske mozog egydimenzionális, a Schrődinger egyenletnek az egydimenzionális formája alkalmazható:

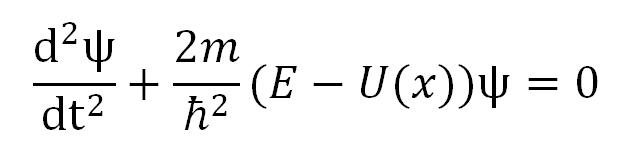
Több gyakorlati esetben a potenciális energia formája ismeretlen vagy annyira összetett, hogy nem lehetséges megtalálni az analitikus megoldást. Egyedül a Schrődinger egyenlet numerikus megoldása lehetséges.

A szabad részecske mozgása

A szabad részecske mozgás ideje alatt, melyre nem hat semmilyen mező, egyenlő a részecske mozgási energiájával. Amennyiben a részecske az x-tengely irányában mozog a Schrődinger egyenlet a következő stacionáris formáját lehet alkalmazni:

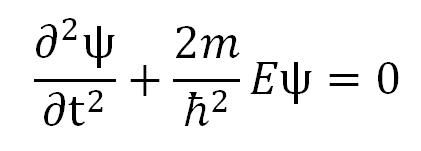
A megoldás ψ(x) = Aexp(ikx) a következő energiaértékekkel E = ħ²k²/(2m). Ez esetben a részecske energiaértéke tetszőleges lehet, illetve az energiaspektruma folyamatos (kontinuális).

Čestica u potencijalnoj jami beskonačne dubine

Ukoliko se posmatra jedan klasičan slučaj koji se odnosi na kuglicu u jami. Ukoliko se kuglica dovede do ruba jame i pusti, onda će se ona kretati unutar ove jame i ne postoji način da je ona napusti. Kaže se da je kuglica "zarobljena" u ovoj jami i da ona može da se kreće samo unutar nje. Ako bi se kuglici, dovedenoj na rub jame saopštila neka početna brzina onda bi ona ona mogla da napusti jamu. Očigledno da je u ovom slučaju klasične fizike kuglica i fizički (prostorno) i energetski zarobljena u jami.

U kvantnoj mehanici pod potencijalnom jamom se podrazumeva prostor u kome se mikročestica može slobodno kretati. Ovaj prostor je ograničen poljem koje ne dozvoljava mikročestici da ga napusti.

Jedan od idealizovanih slučaja, za koji je moguće naći analitičko rešenje Šredingerove jednačine, je kretanje čestice u potencijalnoj jami beskonačno visokih zidova, za koju potencijalna energija ima oblik:

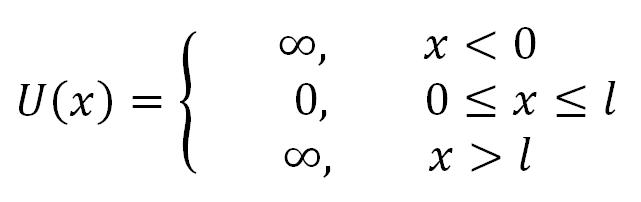
gde je l širina jame, a energija se računa od njenog dna. Pretpostavlja se da se mikročestica (elektron) kreće duž x-ose.

Šredingerova jednačina za ovaj jednodimenzionalni slučaj je:

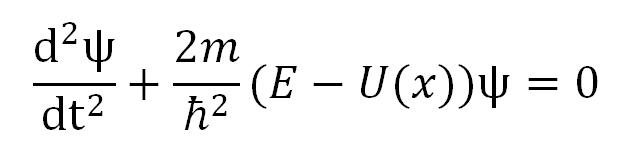
Iz uslova zadatka (beskonačno visoki zidovi) proizilazi da čestica ne može napustiti oblast jame. Prema tome verovatnoća nalaženja čestice (a time i talasna funkcija) za oblast van jame jednaka je nuli. Na granicama jame (pri x = 0 i x = l), zbog neprekidnosti talasne funkcije, vrednost Ψ jednaka je nuli. Dakle, granični uslovi u ovom slučaju su:

ψ(0) = ψ(l) = 0

U oblasti jame (0 ≤ x ≤ l) Šredingerova jednačina se svodi na jednačinu oblika:

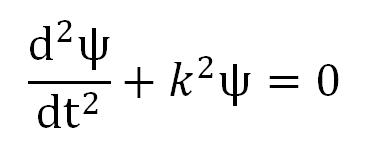
gde je k² = 2mE/ħ² . . (1)

Opšte rešenje diferencijalne jednačine može se napisati u sledećem obliku:

ψ(x) = Asin(kx) + Bcos(kx)

Iz uslova ψ(0) = 0 se dobija:

ψ(0)=0 sledi da je 0=Asin0+Bcos0=B iz čega se zaključuje da je B=0

Talasna funkcija koja je rešenje Šredingerove jednačine dobija oblik:

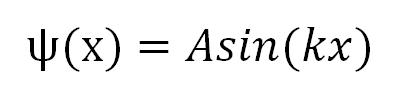
Uslov ψ(l) = A sin(kl) = 0 je ispunjen samo kada je kl = nΠ, gde je n ceo broj:

k = nΠ/l . . (2)

Iz izraza (1) i (2) sledi:

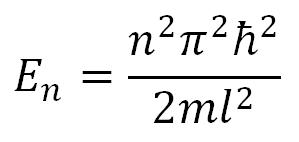
tojest da je Šredingerova jednačina, koja opisuje kretanje slobodne čestice u potencijalnoj jami sa beskonačno visokim zidovima, zadovoljena samo za svojstvene vrednosti E_n koje zavise od celog broja n. Prema tome, energija E čestice u potencijalnoj jami sa beskonačno visokim zidovima ne može biti proizvoljna, već ima diskretne vrednosti (kvantovana je). Kvantovana vrednost energije E_n naziva se energetski nivo, a broj n koji određuje energetski nivo naziva se kvantni broj. Ovo pokazuje da se mikročestica u potencijalnoj jami sa beskonačno visokim zidovima može nalaziti samo na određenim energetskim nivoima tojest u određenim kvantnim stanjima n.