4. razred - Fizika

Ajnštajn za početnike

Od osvita ljudske civilizacije osnovna briga ljudi bilo je obezbeđivanje hrane i uslova za život. Bez obzira na mnogobrojne svakodnevne probleme gotovo je nemoguće naći nekog pripadnika ljudske vrste koji je ikada hodao ovom planetom a da se bar jednom nije zapitao o smislu njegovog postojanja, i postojanja sveta uopšte. Svim ljudima je od davnina poznato da se svi događaji u prirodi odigravaju na nekom mestu, u neko vreme, i najčešće na isti ili sličan način. Svakog jutra na istoku izlazi Sunce, tokom dana putuje preko plavog neba ka zapadu, gde uveče zalazi, noću istim tim nebom putuju zvezde, u proleće biljke dobijaju zeleno lišće, u jesen to lišće žuti i pada na zemlju. Svi ovi događaju odigravali su se davno u prošlosti, u doba naših dalekih predaka, ali sve ovo dešava se i danas. Svi ljudi pojmove prostora i vremena koriste gotovo svakog dana, kada govore o svojim planovima, trenutnom poslu, ili o onome šta su nekada radili. Na prvi pogled tu je sve jasno, ali ako bi nekoga zapitali šta je to prostor a šta vreme, teško da bi ste dobili neki odgovor, a onaj kome je pitanje upućeno našao bi se pred velikim problemom.

Prvi čovek koji je probao da objasni prirodu – prostor, vreme i zakone koji upravljaju njome, bio je Aristotel i to još u davnom III veku pre nove ere. Aristotelovo učenje nije bilo ni nalik onome kako mi danas opisujemo prirodu i pojave u njoj. On je smatrao da se priroda oko nas, svi njeni zakoni, mogu opisati prostim razmišljanjem i zaključivanjem, bez ikakve potrebe da se rezultati tog razmišljanja provere u praksi. Dugotrajnim posmatranjem prirode i razmišljanjem došao je do nekih važnih zakona i ideja.

Tvrdio je da je svet sagrađen od četiri elementa: zemlje, vode, vatre i vazduha, sva kretanja u prirodi bila su posledica težnje ovih elemenata da zauzmu svoje prirodno stanje. Verovao je da tela padaju na Zemlju zbog toga što je za njih “prirodno” da se tako ponašaju, zemlja je pretstavljala njihov prirodan položaj, to je bilo mesto gde su ona pripadala, pa je zato to bio pravac gde su ona želela da idu. U slučaju vatre Aristotel je smatrao da dim, koji se pretežno sastoji od vazduha, teži ka svom prirodnom položaju, tj. vazduhu, i zbog toga se udaljava od zemlje, odnosno kreće se na gore. U Aristotelovim učenjima takođe stoji da je prirodno stanje tela stanje mirovanja. Sva tela miruju dok ih neka sila ne primora da to stanje promene (Aristotel pojam sile ne koristi u nama poznatom značenju, kao interakciju između tela, već on smatra da je sila “želja” nekog tela ka svom “prirodnom” stanju). Prema Aristotelovim zakonima teža tela padaju brže nego lakša zbog toga sto ona imaju veću “želju” ka prirodnom položaju, tj. ka zemlji.

Aristotel je postavio i neke osnovne zakone kretanja, ali on te zakone nije postavio na način kako se to danas radi, korišćenjem matematičkih formula, već je on svoje ideje i zakone izložio običnim jezikom kojim su govorili svi ljudi. Aristotelovi zakoni fizike glase:
I zakon (zakon inercije) – Svako telo na koje ne deluje nikakva sila nalazi se u stanju apsolutnog mirovanja.
II zakon (zakon kretanja) – Sila je proporcionalna brzini (F = mv)
III zakon (zakon gravitacije) – Teža tela padaju brže nego lakša tela

U svom poznatom delu “Na nebesima” Aristotel je pisao o tome kako Zemlja nije ravna ploča već da je ona okrugla, čak je uspeo da izračuna i relativno tačan obim naše planete. Osim toga Aristotel je objavio i, može se reći, prvi model univerzuma – u njegovom centru nalazila se Zemlja, a Sunce, Mesec, planete i sve zvezde su kružile oko nje.

U doba Aristotela, a i mnogo vekova kasnije, Aristotelovi zakoni su bili neprikosnoveni. Niko nije sumnjao u njihovu ispravnost, niti je nekom padalo na pamet da proba da proveri ove zakone fizike. Kada se prvi put javila sumnja u ispravnost Aristotelovog učenja, i kada je neko po prvi put u proučavanju sveta upotrebio eksperiment, svari su krenule naopako za Aristotela.

Srećom, jednog dana rodio se čovek koji je imao dovoljno hrabrosti da pokaže da je čovečanstvo nekoliko vekova živelo u zabludi. Taj čovek bio je Galileo Galilej. Rođen u Italiji 1564. godine, iste godine kada je rođen Šekspir, a umro Mikelanđelo. Studirao je medicinu, ali fakultet nikada nije završio. Ceo svoj život posvetio je nekim drugim naukama – fizici i astronomiji. Uz njegovo ime ostaće zapisano verovatno najveći pronalazak u istoriji fizike. Galilej je prvi shvatio važnost eksperimenta i počeo je da vrši različite eksperimente sa željom da proveri ispravnost Aristotelovih zakona.

Prva stvar koja je Galileju smetala u Aristotelovim zakonima bilo je tvrdjenje da masivnija tela padaju brže od onih sa manjom masom. Galilej je hteo da proveri ovaj zakon eksperimentom. Istoričari fizike još uvek ne mogu da se slože na koji način je Galilej vršio taj eksperiment. Svima je verovatno dobro poznata priča o kuglama, Galileju i Krivom tornju u Pizi. Mnogo je onih koji tvrde da je Galilej eksperiment stvarno vršio na tornju, ali ima i mnogo protivnika te ideje, koji tvrde da je Galilej gugle, umesto sa tornja, puštao niz strmu ravan. Teško je utvrditi ko je upravu ali postoji mogućnost da si upravu i jedni i drugi. Stilme Drejk (Stilllman Drake), čovek koji se opredelio da postane biograf Galileja, ima vrlo zanimljivo mišljenje o ovom eksperimentu. On zapravo smatra da je Galilej naučne eksperimente prvo vršio poštajući kugle različitih masa a istih dimenzija da se kotrljaju niz jednu strmu padinu. Ova situacija je identična situaciji sa bacanjem predmeta sa vrha tornja, ali mnogo je lakše izvesti posmatranja zbog toga što su brzine manje. Galilejeva merenja pokazala su da svako telo istom stopom povećava brzinu bez obzira na masu tojest ubrzanje tela nije zavisilo od mase. Kada je eksperimenat ponovio mnogo puta i bio potpuno siguran u ono što dobija preostajao mu je samo još "lakši" deo posla, trebalo je ubediti druge ljude da je Aristotel pogrešio. Umeo je Galilej da smisli i odličan način da rezultate svog eksperimenta demonstrira i drugim ljudima (nema boljeg načina da se ljudi u nešto ubede nego omogućiti im da to vide sopstvenim očima) a za tu demonstraciju služio je upravo Krivi toranj. Naravno Galilej je morao biti siguran u to šta će se tačno desiti pre "javnog nastupa". Nobelovac Lion Ledermen u knjizi “Božija čestica” o ovome piše:

Bilo kako bilo, Galilej je sigurno dobro znao šta radi i uspeo je da ubedi ljude da je Aristotel u ovom slučaju pogrešio.

Sledeća stvar koja je Galileju smetala u Aristotelovom učenju bilo je geocentrični model svemira, tojest povlašćen položaj Zemlje. Koristeći teleskop, koji je sam konstruisao, uspeo je da otkrije mala tela koja kruže oko Jupitera (danas se zna da su ta tela ustvari najveći sateliti Jupitera, koji se nazivaju Galilejevi sateliti). Ovo je bio dovoljan znak za Galileja da ne kruži baš sve oko Zemlje. Zbog ovog "napada" na učenje Aristotela, Galilej se našao pred velikim problemom, došao je u sukob sa Crkvom i inkvizicijom. Bio je primoran da se javno odrekne svog učenja i tako je sebe spasao sudbine Đordana Bruna i spaljivanja na lomači.

Sačuvao je život ali nije sačuvao slobodu, ostatak svog života proveo je u zatvoru.

Umro je kao zatvorenik u sopstvenoj kući 1642. godine, iste godine u Londonu, božićnjeg dana rođen je budući veliki fizičar – Isak Njutn.

Svima je dobro poznato ime Isaka Njutna i sve ono šta je on uradio. Doprinos ovog čoveka razvoju fizike, a može se slobodno reći i ljudske civilizacije uopšte, je neprocenjiv. Svi se sigurno dobro sećaju osnovne škole, prvih časova fizike i tri Njutnova zakona: zakona inercije, osnovnog zakona dinamike i zakona akcije i reakcije. Mnogi su sigurno čuli i priču o Njutnu koji sedi ispod drveta, i najpoznatijoj jabuci na svetu, koja je dovela do zakona gravitacije. Taj zakon gravitacije je, može se reći, prvo objedinjenje fizike, tim zakonom njutn je pokazao da je ista sila odgovorna i za padanje jabuke i lišća i za kretanje Meseca i planeta. Teško je pisati o čoveku kakav je Njutn bio, nemoguće je opisati značaj njegovih otkrića. Dok hodamo ulicom, putujemo automobilom, vozom, avionom, dok astronauti lete u svemir, dok šalju letilice ka drugim planetama Njtnovi zakoni "rade" i "kontrolišu situaciju".

Neko možda sada izgleda da je Njutn postigao savršenstvo u fizici, ali nije. Mnogo vremena je prošlo od kada je Njutn postavio ove zakone i mi ih još uvek stalno koristimo, ali krajem XIX i početkom XX veka ljudi su videli da postoje i takve situacije u prirodi koje Njutnovi zakoni ne mogu da objasne, fizika je opet klrenula putem razvoja.

Počeci teorije relativnosti

I Aristotel i Galilej i Njutn verovali su u apsolutno vreme. Smatrali su da je moguće izmeniti interval između dva događaja, odnosno da bi ovo vreme bilo isto bez obzira na to ko ga meri, pod uslovom da se koristi dobar časovnik. Vreme je bilo potpuno zasebno i nezavisno od prostora. Za većinu ljudi ovo bi bilo zdravorazumsko stanovište. Pa ipak, ljudi su vremenom morali da promene svoja viđenja prostora i vremena. Iako su, kako izgleda, zdravorazumske predstave sasvim na mestu sa stvarima kao što su jabuke ili planete koje se kreću srazmerno sporo, prestaju da budu ispravne kada su u pitanju stvari koje se kreću brzinom svetlosti ili sasvim blizu nje.

Ideja o stacionarnom etru

Još mnogo godina pre preciznog merenja brzine svetlosti bilo je poznato da je za prostiranje zvučnih, odnosno mehaničkih talasa, neophodno postojanje neke sredine kroz koju bi isti putovali. Postojanje sredine kroz koju talas putuje uslovljeno je time što se talas prostire prenošenjem vibracija sa jedne čestice na drugu. Kao posledica neophodnosti postojanja sredine bilo je poznato da zvučni talasi ne mogu da putuju kroz vakum, a to je i eksperimentalno potvrđeno. Druga vrsta svima poznatih talasa bili su vodeni talasi za čije je prostiranje bila neophodna voda, ovi talasi bez vode koja ih je nosila nisu mogli da postoje. Nakon svega ovoga potpuno je razumljivo zašto su ljudi smatrali da je i za prostiranje svetlosti, odnosno elektromagnetnih talasa, neophodno postojanje neke sredine kroz koju bi ovi putovali, odnosno mora da postoji neka supstanca čije bi čestice vibrirale i na taj način prenosile svetlosni talas.

Ali nasuprot ideji o postojanju neke supstance koja je ispunjavala celokupan prostor univerzuma, pouzdano se znalo da u ogromnom prostranstvu između planeta i zvezda nema nikakvog medijuma, ceo taj prostor bio je vakum. Niko nije mogao da poveruje da svetlost putuje 150 miliona kilometara od Sunca do Zemlje kroz prazan prostor, niko nije verovao da za prostiranje svetlosti nije potreban nikakav medijum, pa su za tog hipotetičkog prenosioca svetlosti stvorili posebnu reč i nazvali su ga lumeniferoznim (svetlosnim) etrom. Prema toj ideju etar je postojao svuda gde su svetlosni talasi putovali, i ispunjavao je sav vasionski prostor koji su do tada svi smatrali da je prazan.

Ideja o postojanju etra je svima delovala vrlo logičnom i ubrzo je etar prihvaćen kao jedan od materijala u vasioni. Neki naučnici su čak išli toliko daleko da su pokušavali da izračunaju gustinu etra!

Majkelson - Morlijev eksperiment

Bez obzira na sve neuspehe u pokušaju detekcije etra niko nije dovodio u sumnju njegovo postojanje. Svi su smatrali da je potreban mnogo osetljiviji eksperiment. Takav eksperiment zamislili su i izveli Majkelson i Morli 1881. godine.

Eksperiment koji su Majkleson i Morli izveli zasnivao se na vrlo jednostavnom principu. Ako bi smo zamislili takmičenje dva identična aviona. Neka ta dva aviona istovremeno krenu iz tačke A, jedan ka tački B a drugi ka tački C. Prvi avion treba da leti na sever do tačke B a zatim nazad do tačke A, a drugi na istok do tačke C a zatim nazad u do A. Tačke B i C nalaze na istom rastojanju od A i to rastojanje iznosi 800 km. Maksimalna brzina oba aviona iznosi 1600 km/h i ako nema vetra lako je zaključiti da će trka završiti za jedan sat, nerešenim rezultatom.

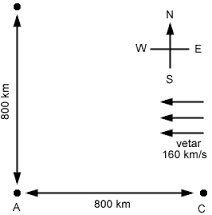
Ako bi sada pretpostavili duva vetar sa istoka ka zapadu brzinom od 160 km/h, trka se ne bi završila bez pobednika, a pobednik bi bio prvi avion. Prvi avion bi pobedio iz razloga što bi drugom avionu vetar koji duva “u lice” dopustio da se kreće brzinom od 1440 km/h jer se njegova maksimalna brzina od 1600 km/h odnosi na miran vazduh. U povratku bi drugi avion imao vetar “u leđa” i njegova brzina bi sada bila 1760 km/h, ali kako više vremena provodi krećući se manjom brzinom njegova prosečna brzina bi bila manja od prvog aviona. Naravno, i prvi avion tokom celog puta ima bočni vetar koji malo skreće avion da bi kompenzovao uticaj vetra, pa vetar i ovde dovodi do usporenja, pa i prvi avion ima prosečnu brzinu nešto manju od 1600 km/h, ali veću od drugog aviona.

Ako bi se izračunala vremena putovanja oba aviona dobija se da prvi avion završava trku za 1h i 18 sec, a drugi za 1 h i 36 sec.

Lako se zaključuje da u slučaju da su pravac i brzina vetra nepoznati oni mogu da se odrede iz rezultata trke. Upravo na tom principu se zasniva i Majkleson-Morlijev eksperiment. Umesto dva aviona Majkelson i Morli su “organizovali” trku dva svetlosna talasa, koji su međusobno bili normalni.

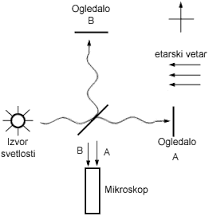
Aparatura koja je korišćena u ovom eksperimentu prikazana je na slici. Aparatura je postavljena tako da se Zemlja kreće u desno i pri tome bi trebalo da se oseti “duvanje” etarskog vetra.

Svetlosni talas kreće od svetlosnog izvora, udara u koso postavljeno ogledalo koje deli talas na dva talasa podjednakog intenziteta. Talas A ide do ravnog ogledala A, a talas B se reflektuje i putuje do ogledala B. Ova dva pojedinačna talasa odgovaraju avionima iz prethodnog primera. talasi reflektovani od ogledala A i B putuju nazad, dolaze do kosog ogledala, i odatle deo talasa odlazi do posmatračevog mikroskopa (interferometra). Posmatrač tada registruje oba talasa u mikroskopu i sve što sada preostaje je “foto-finiš”.

Ako dva talasa ulaze u interferometar i ako su njihovi trbusi i doline poravnati (tj. talasi su u “fazi”) dolazi do njihovog pojačavanja i posmatrač će videti svetliji talas od bilo kog od pojedinačnih. Ovakav rezultat se naziva konstruktivna interferencija. Ako bi se jedan talas našao neznatno ispred ili za drugog, posmatrač bi video nešto tamniji talas od dolazećih. Ovakav rezultat nazvan je parcijalna interferencija. Treća mogućnost koja moče na nastupi nazvana je destruktivna interferencija. Ovaj tip interferencije nastaje kada se bregovi jednog talasa poklope sa dolinama drugog i tada dolazi do međusobnog poništavanja ova dva talasa.

Majkelson i Morli su očekivali da će pod uticajem etarskog vetra doći do pomeranja talasa A i B tako da oni više ne budu u fazi, a posmatrač bi trebalo da vidi svetlost slabijeg intenziteta. Oni su eksperiment izvršili više puta. Ponavljali su ga u različito doba dana i godine, ali rezultati su uvek bili identični – talasi su uvek stizali istovremeno, etarski vetar nije detektovan.

Situacija u nauci je postala prilično zamršena. Čvrsto se verovalo u postojanje etra, ali ne samo što su svi pokušaji da se etar detektuje završili neuspešno. Postojalo je mnogo pitanja, a malo odgovora. Da li etar postoji ili ne? Ako postoji, zašto ga ne možemo detektovati ? A ako ne postoji, zašto ne postoji?

Upravo u takvoj klimi naučnog neraspoloženja i konfuzije dat je odgovor koji je dao veoma jedinstveno, i do tada nezamislivo, objašnjenje da je trebalo biti genije i videti ga. Taj genije bio je Albert Ajnštajn, a sa njim se rodila i Teorija relativnosti.

Specijalna teorija relativnosti

Početkom XX veka Ajnštajnova teorija relativnosti šokirala je svet. Ona je predviđala drastične promene zakona klasične fizike koji su vekovima bili logični, i u čiju ispravnost niko, vekovima, nije sumnjao.

Aristotel, Njutn i svi drugi naučnici pre Anštajna verovali su u apsolutno vreme. Smatrali su, naime, da je moguće izmeriti interval između dva događaja, odnosno da vreme protiče isto za sve posmatrače. Vreme je bilo potpuno nezavisno od prostora. Za većinu ljudi, ovo je sasvim normalno. Ali ipak, čovečanstvo je moralo da promeni svoja viđenja prostora i vremena. Iako su, kako izgleda, ove ideje sasvim u saglasnosti sa stvarima kao što su jabuke ili planete, one prestaju da važe kada se govori o stvarim koje se kreću brzinom bliskom brzini svetlosti.

Ajnštajnova Teorija relativnosti sastoji se od dva glavna dela: Specijalna teorija relativnosti (STR), objavljena 1905. god i Opšta teorija relativnosti (OTR), objavljena 1916. godine. STR razmatra samo predmete ili sisteme (tzv. inercijalni sistemi) koji se, jedni prema drugima, kreću ili konstantnom brzinom ili se uopšte ne kreću. OTR razmatra predmete ili sisteme koji se jedni prema drugima kreću sa određenim ubrzanjem (neinercijalni sistemi).

Postulati Specijalne teorije

Na osnovu rezultata mnogih eksperimenata Ajnštajn je došao do dva vrlo važna zaključka, dva postulata, na kojima je zasnovao celu Specijalnu teoriju relativnosti.

Prvi postulat: svi fizički zakoni izražavaju se u istom obliku u svim sistemima koji se kreću ravnomerno pravolinijski. Ovaj postulat predstavlja tzv. Ajnštajnov princip relativnosti.

Da bi se bolje razumeo pravi smisao ovog postulata setimo se vrlo jednostavne situacije čiji smo svedoci verovatno svi bili. Čovek stoji u vozu i posmatra vagon drugog voza na susednom koloseku. Ako jedan od ova dva voza krene, čovek bi lako mogao da dođe u zabunu koji se voz zapravo kreće. Naravno, ovde je lako odrediti ko se zapravo kreće, potrebno je samo pogledati bilo koji predmet pored pruge, ali zamislimo sada jednog putnika “vozom” u dalekoj budućnosti. Neka on krene sa Zemlje na putovanje, i konstantnom brzinom od 8.000 km/h u odnosu na Zemlju. Dok on tako krstari kroz prostor i izgubi Zemlju iz vida, odjednom iza sebe opaža drugu raketu, i biva iznenađen lakoćom kojim ga ova raketa pretiče. Vozač ove druge rakete čak može da pomisli da se raketa koju zaobilazi uopšte ne kreće! Kako će ovaj “zvezdani putnik” da dokaže da se kreće? Sve što može da odredi je brzina kojom je druga raketa prošla pored njega, i ništa više od toga. Ako bi ova brzina bila 1.600 km/h može se doći do više različitih zaključaka:

• prvi putnik putuje brzinom od 8.000 km/h u odnosu na Zemlju, a drugi je pored njega prošao brzinom od 1.600 km/h
• drugi putnik miruje u odnosu na Zemlju, a prva raketa se kreće unazad, brzinom od 1.600 km/h

Brzo se dolazi do zaključka da je bez korišćenja nekog “nepokretnog” predmeta radi merenja brzine posmatrača nemoguće reći ko se kreće a ko miruje, ako neko uopšte miruje. Ustvari ako bi se posmatrač nalazio negde daleko od svih zvezda i planeta, bez ičega što bi mogao da koristi kao referentnu tačku za merenje brzine, on nikad neće saznati da li se kreće ili ne!

Ovo je bila činjenica do koje je Ajnštajn došao – svako kretanje je relativno. Nikada ne možemo govoriti o apsolutnom kretanju, već samo o kretanju u odnosu na nešto drugo. I uopšte se ne može reći da se neki predmet kreće tom-i-tom brzinom, već se mora reći da ima tu-i-tu brzinu u odnosu na nešto.

Drugi postulat STR kaže da je brzina svetlosti, odnosno maksimalna brzina prenošenja interakcije, ista u svim inercijalnim sistemima. Ovaj postulat je direktna posledica rezultata koji su dobijeni na osnovu Majkelson-Morlijevog eksperimenta. Upravo taj eksperiment je pokazao da bez obzira na pravac prostiranja svetlosti, tojest na način na koji se sistem reference kreće, brzina svetlosti uvek ima istu vrednost.

Ovako, sami po sebi, ovi postulati jesu vrlo zanimljivi ali bez neke veze postulata i realnog sveta, tj bez vormiranja odgovarajućih matematičkih jednačina, koje bi dale vezu između ideje i realnog sveta, oni bi bili zanimljivi ali ubrzo bi bili zaboravljeni. Tu vezu daju upravo jednačine koje se nazivaju jednačine Lorencovih transformacija, jer je Lorenc prethodno došao do istih jednačina na osnovu svoje teorije. Ove jednačine dobro objašnjavaju rezultate onih ekesperimenata koji su naveli Ajnštajna da počne da sumlja u tačnost Njunove teorije, ali što je još važnije jednačine su dale i nova predviđanja, predviđanja koja je kasnije bilo moguće proveriti, i uveriti se u tačnost ove teorije.

Posledice koje predviđaju Lorencove transformacije mogu biti neočekivane i naizgled čudne. Razlog što se Teorija relativnosti uopšte uzev smatra neshvatljivom, nije to što je teško razumeti njene rezultate, nego što je u njih teško poverovati.

Dužina, masa i brzina u specijalnoj teoriji relativnosti

Kontrakcija dužine

Ako bi posmatrač na raketi A bio u mogućnosti da izmeri dužinu rakete B kada se one jedna prema drugoj kreću brzinom v, rezultat koji daju Lorencove transformacije kaže da će B izgledati kao da se skratila, a njena dužina biće data formulom:

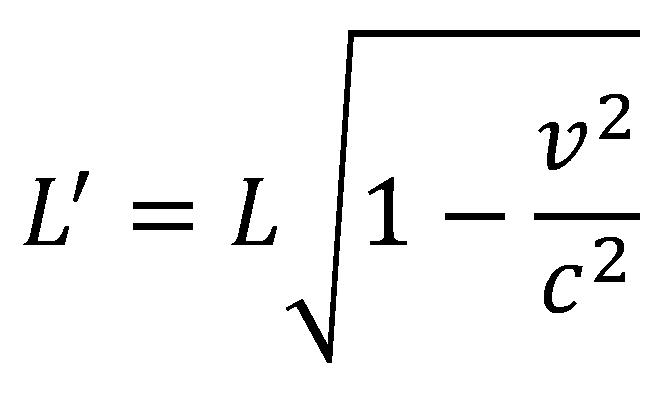
gde je L’ dužina koju A dobija za B, a L je stvarna dužina B, v njihova relativna brzina, a c brzina svetlosti.

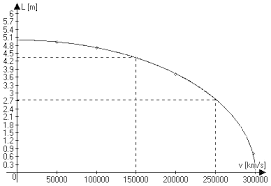
Na slici je prikazana zavisnost dužine rakete, koja je u mirovanju dugačka 100 metara, od njene brzine u odnosu na posmatrača. Sa grafika se vidi da će dužina rakete biti duplo manja pri brzini od 260.000 km/s.

Ista ova formula važi i ako posmatrač iz rakete B meri dužinu rakete A. Na rezultat ne utiče to da li se rakete udaljavaju jedna od druge ili se približavaju. Rezultat zavisi samo od njihove relativne brzine.

Efekat kontrakcije dužine zapaža se samo pri brzinama koje su približne brzini svetlosti. Kako su skoro sve brzine poznate na Zemlji u svakodnevnom životu daleko manje od brzine svetlosti nemoguće je zapaziti efekat kontrakcije. Ako bi se na primer avion kretao brzinom od 1.200 km/h u odnosu na posmatrača, na osnovu date formule se može izračunati da će se on skratiti za nekoliko milionitih delova milionitog dela centimetra, otprilike za prečnik jednog atomskog jezgra. Naravno ovoliko malo skraćenje je nemoguće detektovati.

Porast mase sa brzinom

Sa povećanjem brzine ne menja se samo dužina, već posmatrač registruje i mnoge druge promene.

Pretpostavimo sada da rakete A i B imaju jednaku masu kada su na Zemlji i kada miruju jedna u odnosu na drugu. Neka masa raketa iznosi po 1.000 kg. Ako posmatrač iz rakete A meri masu rakete B kada se one relativno kreću, videće da se masa rakete B povećala i da je njen iznos dat formulom:

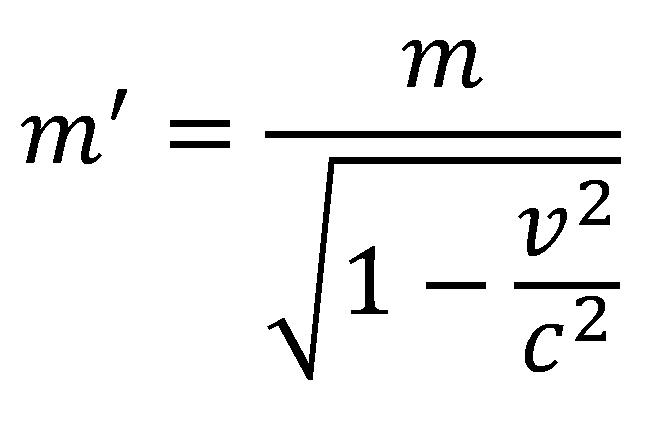
gde je m’ vrednost koju A dobija za masu B, m je prvobitna masa B ili, kako se drugačije ona naziva, masa u mirovanju, v je njihova relativna brzina, a c brzina svetlosti. Na osnovu jednačine (2) dolazi se do zaključka da ako rakete A i B imaju masu od po 1.000 kg dok miruju na Zemlji, onda će kad se budu kretale relativno brzinom od 150.000 km/s izgledati da B ima masu od 1.200 kg posmatrano iz rakete A. Pri brzini od 260.000 km/s posmatrač iz rakete A izmeriće da B ima masu od oko 2.000 kg!

Naravno, treba imati u vidu to da porast mase ne znači da se predmet povećao u smislu fizičkih dimenzija (dužina, širina. visina), čak ne samo da se predmet nije povećao on je postao manji!

Sabiranje brzina

Neka se posmatraču istovremeno približavaju voz i automobil, i to oba brzinom od po 100 km/h u odnosu na posmatrača. Prema tome, ako bi posmatrač merio brzinu voza i automobila dobio bi da ta brzina iznosi tačno 100 km/h. I obrnuto ako bi mašinovođa ili vozač automobila merili svoju brzinu u odnosu na posmatrača dobili bi isti rezultat. Ali, ako bi mašinovođa izmerio svoju brzinu u odnosu na automobil dobio bi da ona iznosi 200 km/h, jer se i voz i automobil kreću u odnosu na nepokretnog posmatrača brzinom od 100 km/h. Isto važi i za vozača automobila, i on se u odnosu na voz kreće brzinom od 200 km/h. Ovakve situacije su vrlo česte u svakodnevnom životu i redovno se koristi jednačina:

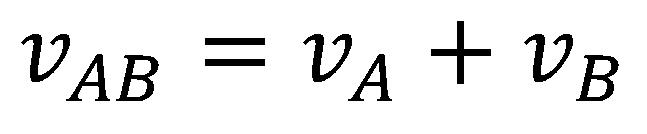
gde je v_AB relativna brzina kojom se A kreće u odnosu na B (tj. brzina voza u odnosu na automobil, ili obrnuto), v_A i v_B su brzine A, tj. B, u odnosu na posmatrača.

Ako bi se posmatrač sada našao u sličnoj situaciji samo što bi umesto voza posmatrao svemirski brod A koji se kreće brzinom svetlosti, a umesto automobila drugi svemirski brod B koji bi putovao brzinom jednakoj polovini brzine svetlosti on bi lako odredio brzine ova dva svemirska broda. Piloti u brodovima takođe lako određuju svoje brzine u odnosu na posmatrača, ali šta će se desiti kada pilot jednog broda, npr. broda B, proba da odredi svoju brzinu u odnosu na drugi brod A? Vođen prethodnom logikom od bi dobio da brzina broda B u odnosu na A iznosi 1,5c, što je nemoguće prema II postulatu. U STR ne važi jednačina za klasičan zakon sabiranja brzina već je neophodno naći novu formulu za sabiranje brzina koja će biti u saglasnosti sa postulatima i Lorencovim transformacijama. Taj novi zakon za određivanje relativnih brzina iskazan je formulom:

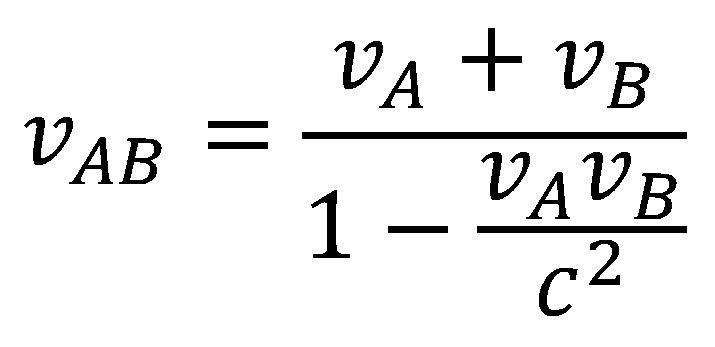
gde su v_A i v_B relativne brzine kojima se A i B kreću prema nepokretnom posmatraču, a c je brzina svetlosti.

Za sve praktične primene klasičan zakon sabiranja brzina se može smatrati ispravnim kada su brzine znatno manje od brzine svetlosti, ali kada su brzine približne brzine svetlosti mora se koristiti prethodna jednačina.

Maksimalna moguća brzina

Od svih predviđanja koja proizilaze iz STR, verovatnije najčudnije je ono da postoji određena brzina preko koje se ništa ne može kretati. Na osnovu jednačine za kontrakciju dužine vidi se da kako brzina raste predmet postaje sve kraći, sve do onog trenutka dok brzina ne dostigne brzinu svetlosti, a tada je dužina jednaka nuli.

Ako pretpostavimo da brzina nastavi da raste, pod korenom bi se našao negativan broj. Kako je kvadratni koren iz negativnog broja imaginaran broj to znači da će i dužina predmeta biti imaginarna, tj. predmet neće postojati.

Slično je i sa masom tela, kako je brzina sve bliža brzini svetlosti masa je sve veća. Onog trenutka kada bi telo dostiglo brzinu jednaku brzini svetlosti masa bi postala beskonačno velika.

Iz ovoga moguće je izvući samo jedan zaključak – brzina svetlosti je maksimalna moguća brzina. Nijedan predmet ne može putovati brže od svetlosti, jer ne samo što mu se dužina smanjuje na nulu nego će i njegova masa postati beskonačno velika. Ustvari, tačnije je reći da se materijalni predmeti koji su poznati u svakodnevnom životu nikada ne mogu kretati brzinom svetlosti jer bi njihova masa tada postala beskonačno velika, što znači da bi bilo potrebno beskonačno mnogo energije da se dovedu do te brzine.

Ekvivalentnost mase i energije

Najznačajnije predviđanje STR bilo je to da je srazmerno mala količina mase ekvivalentna ogromnoj količini energije. Danas je dobro poznato da je prvi ubedljiv dokaz ovog predviđanja bila eksplozija prve atomske bombe kod Alamogorda (Nju Meksiko, SAD) 16. jula 1945. godine.

Kako STR predviđa da sa porastom brzine raste i masa tela, zaključuje se da i energija tela mora da raste jer masivniji predmet ima veću energiju od lakšeg ako su im brzine jednake. Moguće je pokazati da je dodatna energija, koja je povezana sa dodatnom masom, jednaka porastu mase pomnoženim sa kvadratom brzine svetlosti. Na osnovu ovakvog razmišljanja Ajnštajn je zaključio da je sva masa povezana sa energijom, a ta veza data je njegovom čuvenom formulom:

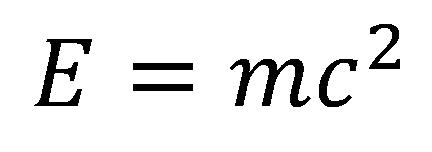
gde je E ekvivalentna energija, m masa tela, a c brzina svetlosti. Na primer, ako bi se u jednačinu uvrstio 1 kg uglja, za energiju se dobija 250 milijardi kilovat-časova, to je približno jednako energiji koju proizvedu sve elektrane u SAD za mesec dana. Kafena kašičica ugljene prašine bila bi dovoljna da najveći brod koji plovi okeanima nekoliko puta pređe rastojanje od Njujorka do Evrope i natrag.

Iz svakodnevnog života svima je poznato da se prilikom sagorevanja uglja oslobađa neuporedivo manja količina energije. Prilikom običnog sagorevanja uglja energija koja se oslobađa nastaje kao rezultat hemijskog procesa, dolazi samo do preuređivanja i novog vezivanja atoma i molekula, ali ne dolazi do merljive konverzije mase u energiju jer se ugalj pretvara u čađ, pepeo, dim, a ne nestaje. Kad bi se svi ovi krajnji produkti izmerili njihova ukupna masa opet bi bila 1 kg.

Vreme u specijalnoj teoriji relativnosti

Specijalna teorija relativnosti je podstakla mnogo drugačiji način razmišljanja o prostoru. Pokazala je da dužina, masa i energija nisu stalne već da su ove veličine usko povezane sa brzinom. Ali, možda najveći doprinos STR bio je vezan za doprinos koji je dala drugačijem shvatanju pojma vremena.

Kako se prema STR ponaša vreme može se videti na istom primeru koji je i do sada korišćen. Časovnici na raketama A i B pokazuju isto vreme u trenutku kada su rakete jedna pored druge, neka je, na primer, u tom trenutku bilo 12 časova. Ovo početno vreme može se nazvati nultim vremenom.

Kako vreme prolazi, rastojanje između A i B se povećava pošto se rakete kreću relativno jedna u odnosu na drugu, i posle nekog konačnog vremenskog intervala rastojanje između rakete A i rakete B iznosiće x. Ako posmatrač na A tada pogleda na svoj časovnik i uporedi sa časovnikom na B, biće iznenađen zato što ova dva časovnika ne pokazuju isto vreme – onaj koji se nalazi na B kasni. Ovu pojavu predviđa STR jer matematički rezultati pokazuju da se vreme koje pokazuju časovnici ponaša prema jednačini:

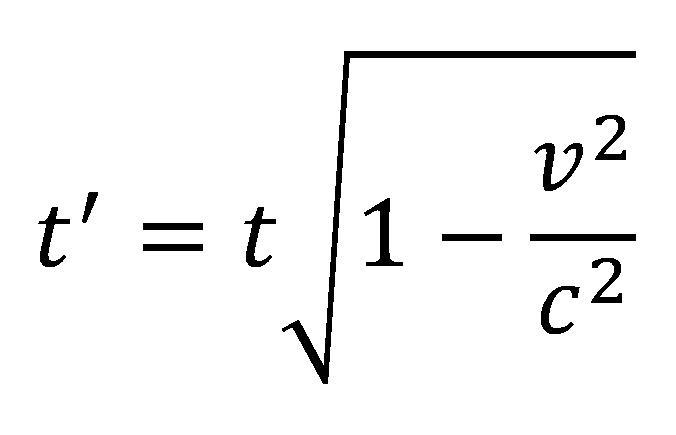
gde je t’ vreme koje posmatrač A “vidi” na časovniku B, a t vreme koje posmatrač A očitava na svom časovniku. Što je relativna brzina veća časovnik na raketi B će se kretati sve sporije i sporije, bez obzira da li se rakete približavaju ili udaljavaju.

Ovaj efekat kašnjenja časovnika u STR se naziva dilatacija vremena i ona nastaje onda kada se dva posmatrača kreću relativno jedan prema drugom konstantnim brzinama, tada svakom od njih izgleda da časovnik onog drugog kasni.

Iz ovih primera može se izvesti zaključak da razlog časovnici A i B kasne jadan u odnosu na drugi nije samo u specifičnom ponašanju svetlosnih talasa već i uzrok toga i izvestan vremenski interval neophodan svetlosnim talasima da putuju od jednog do drugog časovnika. Efekat dilatacije vremena odgovoran je za jedan potpuno drugačiji pogled na vreme od onog koji korišćen ranije. STR je pokazala da je vreme različito u sistemima koji se nalaze na velikoj udaljenosti jedan od drugog.

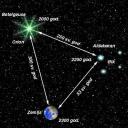
Ako bi dva posmatrača, jedan koji na Zemlji a drugi u blizini zvezde Aldebaran (u sazvežđu Taurus), posmatrali eksploziju supernove na zvezdi Betelgeuse (u sazvežđu Orion). Rastojanje od Zemlje do zvezde Betelgeuse iznosi 300 svetlosnih godina, od Betelgeuse do Aldebarana je 250 svetlosnih godina, a Aldebarana do Zemlje rastojanje je 53 svetlosne godine.

Neka se eksplozija supernove desi na primer 2000 godine. Na Zemlji bi se eksplozija videla tek 300 godina kasnije, jer je svetlosnom talasu koji nosi informaciju o eksploziji potrebno toliko vremena da stigne sa eksplodirale zvezde. S druge strane, u okolini Aldebarana bi isu eksploziju videli 50 godina pre zemljana, jer su oni toliko bliži eksplodiraloj zvezdi.

Lako se uočava činjenica da ovaj događaj nije simultan (istovremen) za posmatrače na tri različita mesta. Osim zbog velikih rastojanja u prostoru do razlike u simultanosti događaja može doći i pri malim rastojanjima ali onda kad su relativne brzine posmatrača približne brzini svetlosti.

Zamislimo sada jednog u vozu koji putuje ogromnom brzinom, približnom brzini svetlosti. Putnik sedi tačno na sredini vagona. Na početku i kraju vagona nalaze se vrata. Kada se vrata otvore pored njih se upali sijalica. U jednom trenutku (istovremeno za posmatrača u vagonu) otvaraju se prednja i zadnja vrata vagona. Posmatrač koji stoji na pruzi, iza voza, neće ova dva događaja videti kao istovremena već će prvo videti onaj koji je njemu bliži, znači prvo će videti da je neko ušao na zadnja vrata vagona pa tek onda na prednja. Ova razlika u odnosu na posmatrača u vagonu posledica je činjenice da je svetlosti koja pokazuje da je neko ušao na prva vrata potrebno da pređe duži put do posmatrača na pruzi i kaže mu: “hej, neko je ovde ušao!”. Ne samo da zavisno od posmatrača ovi događaji mogu da budu istovremeni ili ne, može se desiti da i njihov redosled bude različit – posmatrač koji bi se nalazio ispred voza prvo bi video da je neko ušao na prednja pa tek onda na zadnja vrata.

Naravno treba naglasiti i to da što je veće rastojanje u prostoru između mesta odigravanja dva simultana događaja veća će biti moguća razlika u vremenu između ta dva događaja kako ih vide različiti posmatrači pod različitim uslovima. I obrnuto, ako se rastojanje između dva “istovremena” događaja smanji do iščezavanja, tj. ako se događaji dešavaju na istom mestu, svi posmatrači, bez obzira na njihove položaje i relativne brzine, složiće se u pogledu istovremnosti ovakva dva događaja. Na primer, ako bi došlo do sudara dve rakete, svi posmatrači će videti taj sudar kao jedan usamljen događaj. Bilo bi smešno, a i protivno svim zakonima fizike ako bi bilo koj posmatrač tvrdio da se jedna raketa sudarila pre druge bez fizičkog uzroka.

Na osnovu ovih jednostavnih primera vidi se da stara Njutnova ideja da je vreme svuda isto ne važi baš uvek. Osim toga što istovremenost nije uvek ista, vidimo da čak i redosled događaja nije stalan. Pitate se ko je od posmatrača u ovim primerima upravu – svi su u pravu!

Paradoks blizanaca

Predviđanja specijalne teorije relativnosti o dilataciji vremena navode na neke vrlo zanimljive, a možda i zastrašujuće ideje. Efekat dilatacije vremena mogao bi da ima neke vrlo interesantne primene za vasionska putovanja. STR ne samo da predviđa da će na raketi koja se kreće relativno brzinom bliskoj brzini svetlosti samo vreme proticati sporije, ona takođe predviđa da će SVI procesi biti usporeni. To znači procesi varenja hrane, biološki procesi, atomska aktivnost – sve će biti usporeno!

Zamislimo “zvezdanog putnika” iz daleke budućnosti koji kreće na “godišnji odmor” do zvezde Arcturus (sazvežđe Bootes, Pastir) udaljene 33 svetlosne godine. On ulazi u svoju raketu i kreće na putovanje brzinom približnom brzini svetlosti. Ako stalno putuje tom brzinom na Arcturus će stići za malo više od 33 godine, ali po vremenu na Zemlji Ako bi odmah krenuo natrag na Zemlju bi stigao približno 66 godina nakon odlaska.

Kako se raketa celo vreme kretala ogromnom brzinom u odnosu na Zemlju svi procesi na raketi biće usporeni, putniku u raketi neće izgledati da je proteklo 33 godine za put u jednom smeru, on će stići u blizinu Arcturusa otprilike baš u vreme ručka, a kad se bude vratio na Zemlju izgledaće mu da je prošao samo jedan dan! Ali, ljudima na Zemlji to će biti 66 godina, ljudi na Zemlji će biti 66 godina stariji.

Jedan rezultat koji predviđa STR bio je izvor velike nedoumice i izvesnog neslaganja od vremena svog predstavljanja. To je tzv. paradoks blizanaca ili vremenski paradoks.

Pretpostavimo da od dva blizanca jedan odlazi na putovanje do neke daleke zvezde i natrag a drugi ostaje na Zemlji. Neka je ta zvezda udaljena 4 svetlosne godine od Zemlje, a da se raketa kreće prosečnom brzinom koja je jednaka brzine svetlosti. Ukupno vreme za njeno putovanje biće tada oko 10 godina.

Ako uporedimo brzinu proticanja vremena za blizanca u raketi sa brzinom proticanja vremena na Zemlji, na osnovu jednačine

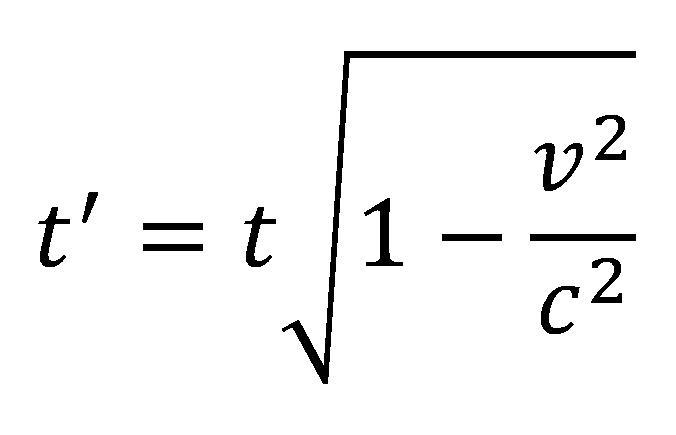
dobija se:

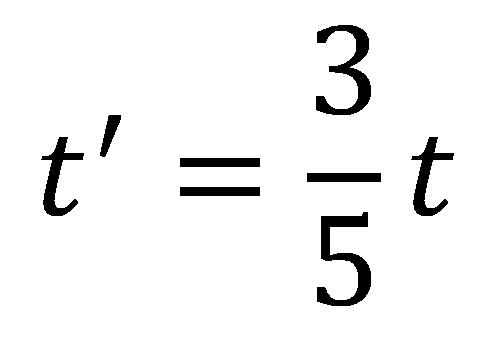
Ovo znači da iako je putovanje trajalo deset godina prema časovniku blizanca na Zemlji, prema časovniku onog u raketi putovanje je trajalo samo šest godina. Po povratku sa puta blizanac će shvatiti da nije ostario onoliko kolko i njegov brat koji je stao na Zemlji.

Paradoks se ovde ogleda u tome da pošto su sva kretanja relativna može da se smatra da je Zemlja otišla u svemirski prostor u pravcu suprotnom od rakete i vratila se dok je raketa mirovala. Na osnovu takvog razmatranja kretanja dolazi se do suprotnog zaključka – blizanac u raketi čekaće 10 godina na povratak svog brata, koji će misliti da je u putovanju (sa Zemljom) proveo samo šest godina.

Očigledno je da ova dva tumačenja ne mogu istovremeno biti tačna. Upravo ova kontradikcija predstavlja tzv. paradoks blizanaca.

Rešenje paradoksa je vrlo jednostavno, tačnije paradoks uopšte ne postoji pošto ove dve situacije nisu simetrične, pa nisu ni matematički reverzibilne. Razlog nepostojanja simetrije je taj što raketa na svom putovanju trpi određena ubrzanja, a pretpostavka da Zemlja odlazi na putovanje nije ispravna jer bi u tom slučaju Zemlja morala da trpi odgovarajuća ubrzanja umesto rakete, a poznato je da se to ne dešava.

STR neizbežno vodi do zaključka da će za vasionskog putnika na kružnom putovanju proći ukupno manje vremena, nezavisno od načina merenja, nego za ljude koji ostaju na Zemlji. Svaki putnik će se na Zemlju vratiti manje ostareo nego oni koji su ostali da ga čekaju. Ukupan iznos usporenja vremena zavisiće od brzine rakete u odnosu na Zemlju i ukupnog pređenog rastojanja za vreme puta.

Do fizičke osnova ovakvog zaključka može se doći poređenjem onoga što svaki blizanac vidi kad posmatra svetlosne talase primljene iz niza događaja koji se dešavaju u sistemu onog drugog.

Tokom prve polovine putovanja, zbog brzine kojom se raketa udaljava od Zemlje, svetlosni talasi događaja na Zemlji stizaće do rakete sporijim tempom, učestalošću, nego kad bi raketa mirovala. Za brzinu rakete od 4/5 brzine svetlosti, ovo usporenje je dato formulom za tzv. relativistički Doplerov pomak, prema kojoj će učestalost biti 1/3 od normalne. Na sličan način za vreme povratka blizanac u raketi posmatra događaje na Zemlji kao da se odigravaju tri puta bržim tempom. Tokom celog putovanja blizanac na raketi registruje događaje na Zemlji kao da se odigravaju prosečnim tempom od 5/3 (što je prosek za od jedne trećine i tri). Znači, rezultat je da blizanac na raketi zapaža da vreme na Zemlji protiče u proseku brže nego na raketi, pri čemu tačan odnos iznosi 5/3, zbog toga će deset godina na Zemlji biti kao šest godina na raketi.

Situacija koju vidi blizanac na Zemlji je obrnuta. On svetlosne talase događaja koji se na raketi odigravaju tokom prve polovine putovanja prima ukupno devet godina. To je zbog toga što raketi treba pet godina Zemaljskog vremena da stigne do zvezde i još četiri godine su potrebne svetlosnim talasima da stignu sa udaljene rakete do Zemlje, jer se raketa nalazi na rastojanju od četiri svetlosne godine. Tokom ovih devet godina blizanac na Zemlji posmatra događaje tri puta sporije od normalnog tempa, u skladu sa relativističkom formulom Doplerovog pomaka.

Događaje koji se odigravaju na raketi tokom povratka na Zemlju blizanac sa Zemlje će posmatrati samo poslednje, desete godine. Za vreme ove poslednje godine on će događaje na raketi videti kao da se odigravaju tri puta brže nego što je to normalno. Ukupan rezultat daje da će događaje koji na raketi ukupno traju šest godina blizanac na Zemlji posmatrati deset godina, odnosno u proseku će vreme na raketi proticati sporije nego na Zemlji.

Iz ovoga se vidi zbog čega fizička situacija nije simetrična za oba blizanca i zašto je ukupno vreme putovanja različito za svakog od njih. Blizanac sa rakete preusmerava svoju brzinu na polovini svog putovanja i počinje da zapaža događaje na Zemlji ubrzanim tempom odmah nakon toga, dok blizanac na Zemlji mora da čeka još četiri godine da svetlosni talasi događaja okretanja rakete stignu do njega pre nego što počne da prima ubrzanim tempom događaje sa rakete. Jednostavnije rečeno, zemaljski blizanac prima svetlosne talase događaja na raketi sporijim tempom ali duže vreme nego blizanac u raketi one sa Zemlje. Efekat ove asimetrije je da zemaljski blizanac posmatra manje događaja koji se dešavaju na raketi, nego što blizanac na raketi posmatra događaja na Zemlji za vreme celog putovanja.

Moglo bi izgledati da su zaključci koji proizilaze iz ovakvog putovanja u suprotnosti sa predviđanjem STR da je brzina svetlosti maksimalna brzina. Kako je putovanje dugo osam svetlosnih godina, a raketa ga prelazi za šest godina putovanja zabeleženim na raketi, prostim izračunavanjem brzine (deljenje pređenog puta sa utrošenim vremenom) dobija se da brzina kojom se raketa kretala za jednu trećinu veća od brzine svetlosti. U čemu je ovde greška?

Razlog zbog čega se javlja “prekoračenje” brzine svetlosti je to što raketa u stvari ne prelazi rastojanje od osam svetlosnih godina. Kao posledica brzine rakete rastojanje do zvezde biće skraćeno za blizanca u raketi usled Ficdžerald-Lorencove kontrakcije, pa na osnovu toga korišćenjem jednačine

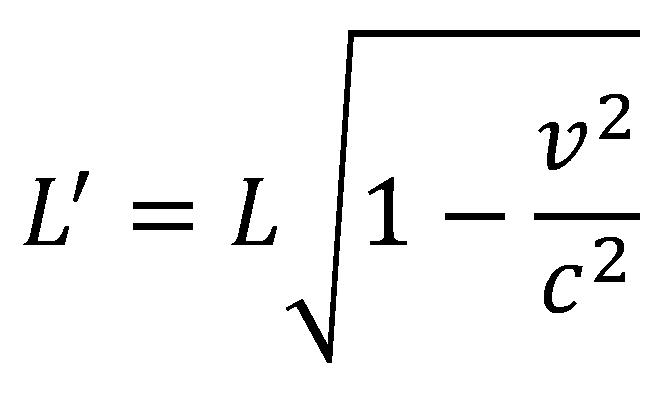
i numeričkih vrednosti iz ovog primera dobija se skraćeno rastojanje od 4,8 svetlosnih godina za povratno putovanje. Deljenjem tog iznosa sa vremenom provedenim u putu, tj. sa šest godina, lako se utvrđuje da prosečna brzina stvarno iznosi 4/5 brzine svetlosti.

Opšta teorija relativnosti

Vec smo se upoznali sa osnovnim idejama Ajnštajnove specijalne teorije relativnosti. Videli smo da ta teorija dobro objašnjava "čudno" ponašanje svetlosti. Ovom teorijom Ajnštajn je uspeo da objasni rezultate Majkelson-Morlijevog eksperimenta, objasnio je zašto je brzina svetlosti ista za sve posmatrače bez obzira na to gde se oni nalazili i kada vršili merenje. Takođe smo videli i šta se dešava sa telima koja se kreću brzinama bliskim brzini svetlosti, i zbog čega je ta brzina maksimalna moguća brzina u prirodi.

Bez obzira na sva ova objašnjenja koja je Specijalna teorija dala ona je otvorila i jedan nov problem. Ova teorija bila je nesaglasna sa Njutnovom, klasičnom, teorijom gravitacije. Prema Njutnovoj teoriji sva tela se međusobno privlače izvesnom silom koja zavisi samo od njihove mase i njihovog međusobnog rastojanja. U ovoj klasičnoj teoriji interakcija, delovanje jednog tela na drugo, prenosi se beskonačno velikom brzinom. Vidimo da je ova činjenica, inače jedna od osnovnih ideja Njutnove mehanike, u suprotnosti sa Specijalnom teorijom koja kaže da se ništa ne može kretati brže od svetlosti. Više puta, između 1908. i 1914. godine, Ajnštajn je pokušao dadođe do teorije gravitacije koja bi bila "pomirila" Njtnovu klasičnu teoriju gravitacije i Specijalnu teoriju relativnosti. Godine 1915. Ajnštajn je postigao uspeh u svom radu. Tada je čovečanstvo dobilo jednu od fizičkih teorija koja je kasnije zadala mnogo muka onima koji su došli posle Alberta Ajnštajna. Bila je to Opšta teorija relativnosti (OTR).

Princip ekvivalencije

Opšta teorija relativnosti je jedna vrlo značajna i komplikovana teorija, ali ova teorija se zasniva na jednom vrlo jednostavnom zaključku.

Setimo se jedne svakodnevne situacije – vožnje liftom. Svi su verovatno nekada primetili kako, dok se voze liftom, nekada izgube osećaj o težini nekog predmeta koji drže u rukama. Na primer, zamislimo jednog putnika koji se vozi liftom sa vrha jednog velikog trgovačkog centra do izlaza na prizemlju. Takođe, zamislimo da se ovaj putnik vraća kući iz kupovine i u ruci nosi tešku torbu punu različitih stvari koje je kupio. Ulazeći u lift on razmišlja o tome šta je sve kupio i koliko je para potrošio. Zatvara vrata i lift kreće nadole. Odjednom putnik je zbunjen – izračunao je da je potrošio puno para a torba je suviše laka? Ali posle kraćeg vremena primećuje da torba ipak ima onu težinu koju bi otprilike i trebala da ima. On silazi do prizemlja, seda u kola i odlazi do svog stana, ulazi u lift svoje zgrade. Lift kreće na gore i... putnik sada primećuje da je torba postala mnogo teška ?

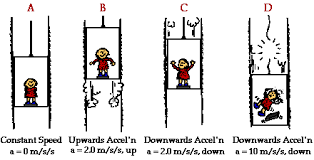
Iz ovog jednostavnog primera primećujemo da težina nekog predmeta nije stalna već da zavisi i od nekih drugih faktora (naravno, treba napomenuti da je ovde težina sila a ne masa, koja se u svakodnevnom životu pogrešno naziva težinom), na primer ubrzanja koje ima lift. Ovaj osećaj promene težine predmeta u liftu nije subjektivan osećaj već realna fizička pojava. Kada bi u liftu bila vaga, koja umesto putnika, meri težinu nekog predmeta u zavisnosti od kretanja lifta težina bi bila različita – kada lift ubrzava naviše predmet bi bio teži, a kada ubrzava naniže predmet bi postao lakši. U slučaju kada bi lift naniže ubrzavao istim onim ubrzanjem koje imaju tela koja slobodno padaju težina predmeta u njemu ni bila jednaka nuli a u liftu bi vladalo bestežinsko stanje, a ako bi ubrzanje bilo još veće svi predmeti bi "pali" na plafon lifta. Kada lift miruje ili se kreće ravnomerno nijedan od ovih efekata ne postoji.

Težina tela je sila kojom Zemlja privlači svako telo, ono što se u prethodnom primeru menja je upravo ta sila, dok masa tela ostaje uvek stalna. Ajnštajn je uvideo ovu povezanost između ubrzanja i sile teže i došao do revolucionarnog zaključka – u jednoj tački prostora efekti gravitacije i ubrzanog kretanja su ekvivalentni i ne mogu se međusobno razlikovati. Upravo ovaj zaključak predstavlja princip ekvivalencije.

Na osnovu ovog principa zaključujemo da se efekti povećanja težine putnika u liftu mogu izazvati i promenom gravitacije. Zamislimo da možemo lift sa putnikom, bez njegovog znanja, da prebacimo na Mesec. Kako bi se tada naš putnik uplašio na šta je potrošio pare u kupovini kada je torba toliko laka!

Sam po sebi princip ekvivalencije je jednostavno zapažanje, ali on sam nije mogao da dovede do postavljanja jedne od najvažnijih i najčudnijih fizičkih teorija XX veka. Da bi došao do Opšte teorije Ajnštajn je morao da primeni i jedan, tada nov, matematički aparat – tenzororski račun, koji je nešto ranije razvio Riman. Na ovaj način Ajnštajn je uspeo da dođe do tri veoma važna zaključka, a što je najvažnije svi ti Ajnštajnovi zaključci, ma koliko čudni tada izgledali, kasnije su i eksperimentalno potvrđeni.

Ajnštajnova teorija gravitacije

Prvi zadatak i prva provera Opšte teorije relativnosti bilo je tačno opisivanje orbita planeta oko Sunca. Mnogo godina pre Ajnštajna Njutnova teorija gravitacije je dobro opisala orbite planeta. Vremenom tehnika posmatranja i instrumenti su postajali sve precizniji i videlo se da rezultati za kretanje planeta koje daje klasična teorija ne odgovaraju u potpunosti pravom stanju stvari u Sunčevom sistemu. Bilo je poznato da na kretanje planeta oko Sunca utiče jedino sila gravitacije, a kako je Opšta teorija teorija gravitacije ovo je bio prvi test za njenu proveru.

Rezultati koji su dobijeni primenom Ajnštajnove teorije su bili približno isti kao i rezultati koje je dala klasična teorija, ali bilo postojala je i jedna velika razlika. Obe ove teorije predviđaju da se planete oko Sunca kreću po eliptičnim putanjama, ali za razliku od klasične teorije opšte teorije relativnosti pokazuje da te elipse nisu stacionarne već da one rotiraju oko Sunca. Posmatrano u dugom vremenskom intervalu može se videti da planete, na svom putovanju oko Sunca, opisuju putanju oblika rozete.

Sada je trebalo proveriti rezultate koje je dala opšte teorije relativnosti. Brzina kojom elipse rotiraju oko Sunca je vrlo mala, gotovo nemerljiva. Da bi se proverila ova teorija bilo je neophodno vršiti vrlo precizna merenja i to na orbiti planete koja najbrže rotira. Teorija je pokazala da rotacija orbite treba da bude najveća za planete sa najvećom orbitalnom brzinom, ali bilo je neophodno posmatrati i planetu sa dovoljno izduženom orbitom kako bi rotacija orbite bila vidljiva (orbite većine planeta su skoro kružne). Srećom, u našem planetarnom sistemu postoji jedna planeta koja je ispunjavala oba uslova. To je Merkur, za koju je opisivanje orbite već zadavalo puno problema astronomima. Mnogo godina ranije bilo je poznato da orbita ove male planete rotira za 574 lučnih sekundi svakih 100 godina. Astronomi su uspeli da objasne postojanje rotacije od 531 sekunde kao posledicu gravitacionog uticaja ostalih planeta. Preostalo je još 43 lučne sekunde koje je bilo nemoguće objasniti. Bilo je pokušaja da se ova razlika pripiše postojanju jedne nove, neotkrivene planete, ali svi pokušaji da se ta planeta nađe bili su bezuspešni.

Sve do objavljivanja opšte teorije relativnosti uzrok ovakvog ponašanja Merkurove orbite bio je misterija, ali kada su astronomi primenili ovu teoriju za opisivanje putanje Merkura dobijena je upravo vrednost koju su davala i posmatranja. Bio je ovo prvi trijumf Opšte teorije relativnosti.

Značenje zakrivljenog prostor-vremena

Iz gore navedenih rezultata može se pogrešno zaključiti da razlika između klasične teorije i Opšte teorije relativnosti nije velika. Ipak, razlika između ovih teorija je ogromna, suštinska. Razlika ne leži u tome što su brojni rezultati različiti već je njihova razlika u načinu na koji opisuju sam pojam gravitacije. Njutnova teorija gravitaciju shvata kao jednu sasvim običnu silu, ali Ajnštajn potpuno odbacuje ovo tvrđenje. U Opštoj teoriji gravitacija više nije sila već je ona osobina samog prostor-vremena. Gravitacija je rezultat toga što, prema ovoj teoriji, prostor-vreme nije ravno već je zakrivljeno pod uticajem raspodela masa i energija u njemu. Negde daleko u vasioni, daleko od svih masivnih objekata prostor i vreme su savršeno ravni, ali približavanjem nekom masivnom objektu ulazi se u oblasti sve veće i veće zakrivljenosti prostor-vremena. Jačina gravitacionog polja je zapravo mera zakrivljenosti prostor-vremena.

U ovom novom, na ovaj način definisanom, prostor-vremenu planete se zapravo kreću po pravim putanjama, a njihove putanje nama izgledaju zakrivljeno zbog oblika samog prostora. Putanje kojima se tela kreću u ovom zakrivljenom prostor-vremenu nazivaju se geodezijske linije, a te linije predstavljaju najkraće rastojanje između dve proizvoljne tačke. Da bi smo bolje razumeli šta ovo zapravo znači posmatrajmo površinu Zemlje kao jedan zakrivljeni dvodimenzionalni prostor. Ako bi probali da na globusu povučemo najkraću liniju između dva grada primetili bi da ta linija nije prava već je kriva, ali kada bi zatim seli u avion i krenuli u pravcu koji smo nacrtali nama bi izgledalo da putujemo po pravoj liniji, i kada ne bi smo znali da je Zemlja okrugla teško bi neko mogao da nas ubedi da ne putujemo po pravoj već po krivoj liniji. Slična ovakva situacija je i sa četvorodimenzionalnim prostor-vremenom.

Jednostavno rečeno opšte teorije relativnosti nam pokazuje da materija saopštava prostor-vremenu kako da se savije a savijeno prostor-vreme saopštava materiji kako da se ponaša.

Bila je ovo još jedna čudna i, na prvi pogled, totalno neprihvatljiva ideja koju nam je dala Ajnštajnova teorija relativnosti. Retko ko je mogao da poveruje u ovo, i Ajnštajn je to sasvim dobro znao pa je odmah predložio i način da se njegova tvrdnja proveri i na taj način sa sigurnošću potvrdi da mi živimo u zakrivljenom četvorodimenzionalnom prostor-vremenu.

Eksperiment koji je Ajnštajn predložio zasnivao se na tome da je on trebalo da pokaže da svetlosni snop koji dolazi sa neke udaljene zvezde skreće sa početnog pravca dok prolazi pored Sunca.

Da bi izvršili ovo merenje astronomi su praktično trebali da izmere koju težinu ima svetlosni snop na Suncu. Kao i svi drugi predmeti tako i svetlost ima neku težinu. Svetlosni snop sastoji se od mnoštva čestica, tzv. fotona koji imaju izvesnu masu kada se kreću. Svima je poznato kako je moguće izmeriti masu bilo kog tela iz svakodnevnog života koje se kreće – pokupimo ga kada padne i stavimo na vagu. Ali sa fotonima nije tako lako. Ne samo da je nemoguće uhvatiti fotone i staviti ih na vagu već fotoni uopšte i nemaju masu kada miruju, oni postoje samo kada se kreću. Ovo merenje je, teorijski gledano, vrlo jednostavno – ako gravitaciono polje utiče na fotone putanja svetlosnog snopa biće zakrivljena što je lako utvrditi ako je zakrivljenost dovoljno velika, ali ako gravitaciono polje ne utiče na fotone oni će nastaviti da putuju bez skretanja, što je opet lako detektovati. Na ovaj način može se odrediti pravac prostiranja svetlosti, a samim tim i geometrija prostora. Da bi se ovo merenje izvršilo neophodno je posmatrati skretanje svetlosnog snopa koji prolazi pored nekog masivnog tela jake gravitacije, a najbolji kandidat, kojim raspolažemo, za ovakvo merenje je Sunce.

Svetlosni snop koji se posmatra mora da dolazi sa neke udaljene zvezde. Onda kada između Zemlje i zvezde nema nikakvih masivnih objekata i gravitacionog polja snop svetlosti će se do nas kretati pravolinijski. Pretpostavimo da, posle nekog vremena, krećući se oko Sunca, Zemlja dođe u takav položaj da svetlosni snop sa zvezde skoro dotiče površinu Sunca.

Ovde se opet javlja veliki problem jer je, zbog ogromnog sjaja Sunca, nemoguće videti bilo koji zvezdu iza njega. Da bi rešio ovaj problem Ajnštajn je predložio da se merenje vrši tokom totalnog pomračenja Sunca.

Postupak merenja se sastojao u tome da je zvezde prvo trebalo fotografisati kada tu nema Sunca a zatim se isti postupak ponavlja za vreme totalnog pomračenja. Na ovim novim fotografijama, ako je opšta teorija relativnosti tačna, zvezde u blizini Sunca bi trebale da budu pomerene u odnosu na položaj na prvoj fotografiji. Ajnštajn je izračunao da ovo pomeranje prividnog položaja zvezde treba da bude 1,74 lučne sekunde.

Najpovoljnije pomračenje Sunca za ova merenja desilo se 29. maja 1919. godine. Posebna pogodnost ovog pomračenja bila je u tome što su krajem maja Zemlja i Sunce poravnati sa mnoštvom sjajnih zvezda pa je lako izabrati neku od njih za merenja. Za ovu izuzetnu priliku pripremljene su dve britanske ekspedicije, jednu je vodio A.C.Kromlin i ona je otputovala u severni Brazil dok je druga, pod vođstvom A.S.Edingtona putovala na jedno ostrvo u Gvinejskom zalivu. Za vreme totalnog pomračenja napravljen je ogroman broj fotografija koje su zatim, nakon povratka u Britaniju, detaljno analizirane.

Na fotografijama prve ekspedicije pomeranje zvezda iznosilo je 1,98 lučnih sekundi a na onima koje su snimili članovi druge ekspedicije razlika je bila 1,6 lučnih sekundi. Ovako dobro slaganje izmerenih vrednosti sa rezultatima eksperimenta dobilo je odlična potvrda tačnosti Opšte teorije.

Tokom šest decenija sve preciznijeg ponavljanja ovog i njemu sličnih eksperimenata nisu pronađene eksperimentalne činjenice koje bi osporile tačnost opšte teorije relativnosti. Ogroman broj eksperimentalnih provera je potvrdio da je Opšta relativnost daleko najpotpunija, najtačnija, najelegantnija i najpreciznija teorija gravitacije koju je čovečanstvo ikada imalo.

Gravitacija i vreme

Već je rečeno da Teorija relativnosti ne pravi razliku između prostora i vremena. Do sada smo videli koje su posledice Opšte teorije na "izgled" prostora. Slične ovakve posledice registruju se u proticanju vremena.

Opšta teorija relativnosti predviđa da gravitacija usporava vreme. Samo negde daleko u prostor-vremenu, daleko od svih gravitacionih polja, tamo gde je prostor-vreme potpuno ravno časovnici otkucavaju normalnim tempom. Približavanjem bilo kom masivnom objektu vreme počinje da teče sve sporije i sporije. Na osnovu ovoga može se zaključiti da će vreme na Zemlji proticati nešto brže nego na Jupiteru. Dok će na Jupiteru vreme teći brže u odnosu na Sunce. Ajnštajn je izračunao da jedna sekunda na Zemlji traje 1,000002 Sunčevih sekundi.

Bilo je mnogo pokušaja da se ova razlika izmeri, ali nijedan od njih nije bio uspešan. Prvi eksperiment koji je potvrdio tačnost i ovog tvrđenja OTR izvršen je, verovali ili ne, na Zemlji! Godine 1960, pet godina nakon Ajnštajnove smrti, na Harvardskom univerzitetu, dr Robert Paund i njegov asistent Glen Rebka su izvršili eksperiment koji je potvrdio razliku u brzini proticanja vremena na površini Zemlje i na nekoj maloj visini iznad naše planete (gde je gravitacija nešto slabija). U svom eksperimentu oni su koristili toranj visok 22,6 metara, jedan časovnik se nalazio na Zemlji a drugi na vrhu tornja. Za ovako precizno merenje bilo je neophodno koristiti vrlo precizne časovnike. U prirodi je teško naći precizniji časovnik od atomskog, u ovom eksperimentu časovnici su bila jezgra radioaktivnog Co-57. Kada je sve ovo postavljeno na svoje mesto trebalo je jedino detektrima meriti frekvenciju fotona gama zraka koji su nastajali prilikom radioaktivnog raspada. Rezultati koji su u ovom eksperimentu dobijeni dobro su se poklopili sa onim šta je predvidela Ajnštajnova teorije.

Pet godina nakon smrti njegovog tvorca Ajnštajnova teorija je konačno u potpunosti eksperimentalno potvrđena. Sumlje više nije bilo, čovečansvo je dobilo najbolju teoriju gravitacije koju je ikada imalo. Ali, to što je ova teorija potvrđena kao tačna nije umanjilo interesovanje za nju, naprotiv ona je postala još značajnija i otvorila je jedan sasvim nov pogled na svet.

Fizika ili naučna fantastika

Svako se verovatno zapitao zašto je značaj Teorije relativnosti toliko veliki. Svima je dobro poznato da u svakodnevnom životu "staromodno" Njutnovo shvatanje gravitacije kao sile funkcioniše bez greške. Čak i za slanje ljudi na Mesec, lansiranje svemirskih brodova ka planetama stara Njutnova teorija izvanredno funkcioniše. Zašto se onda mučiti komplikovanim izračunavanjima u Opštoj teoriji relativnosti, kada u svim poznatim situacijama Njutnova teorija daje zadovoljavajuće rezultate?

Vrlo dugo nakon objavljivanja Teorije relativnosti niko nije verovao da u Univerzumu postoji mesto gde Njutnova teorija prestaje da funkcioniše, mesto gde su prostor i vreme toliko zakrivljeni da je neophodno koristiti Opštu teoriju relativnosti. U blizini Zemlje, Sunca, Jupitera i drugih dobro poznatih tela gravitacija je vrlo slaba a prostor-vreme neznatno zakrivljeno pa zato Njutnova teorija daje dobre rezultate.

Tokom 60-tih godina XX veka fizičari su počeli da shvataju evolutivni put zvezda, od rođenja do njihove smrti. U nekim fazama života jedne zvezde, mnogo masivnije od našeg Sunca, Njutnova teorija prestaje da "radi". Pred kraj života jedne takve masivne zvezde gravitacija konačno, u ratu koji je trajao nekoliko miliona godina, pobeđuje unutrašnje sile (toplotno zračenje, elektrostatičko odbijanje) zvezde. Tada zvezda počinje da se smanjuje, a njena gustina i gravitacija počinju da rastu (gravitaciona sila je obrnuto proporcionalna kvadratu rastojanja, znači ako se poluprečnik zvezde smanji dva puta sila poraste četiri puta; masa zvezde se ne menja). Kako gravitacija postaje sve jača i jača prostor-vreme postaje sve više zakrivljeno. Ovaj proces se prvo odvija polako, ali u jednom trenutku, iznenada, gravitacija počinje da savlađuje i i sile između čestica umiruće zvezde. Za samo nekoliko sekundi zvezda se strahovito skuplja, dok njene čestice (protoni, elektroni, neutroni) bivaju zgnječeni jedni u druge. Više ne postoji nijedna sila u prirodi koja bi "pobedila" gravitaciju, zvezda je osuđena da postane crna rupa.

Kako se zvezda sve više približava njenoj neizbežnoj sudbini, sve manje svetlosti uspeva da se otrgne gravitaciji. Zakrivljenost prostor-vremena je toliko velika da samo oni zraci koji vertikalno napuštaju zvezdu uspevaju da pobegnu. Ako bi neko bio u mogućnosti da sa bezbedne daljine posmatra ovu zvezdu izgledalo bi mu da se njen sjaj postepeno smanjuje.

Konačno, u jednoj fazi kolapsa, zakrivljenost postaje toliko velika da svetlost uopšte ne može da napusti zvezdu. Ovo se dešava u trenutku kada gravitacija zvezde postane toliko jaka da je prva kosmička brzine zvezde veća od brzine svetlosti, najveće moguće brzine u prirodi. Kaže se da je zvezda upala u svoj horizont događaja. Termin “horizont događaja” je veoma pogodan. To je doslovno horizont u geometriji prostora i vremena iza kojeg se ne može videti nijedan događaj. Ne postoji nikakav način da se sazna šta se dešava unutar horizonta događaja. To je mesto koje je odvojeno od našeg prostora i vremena, to više nije deo naše vasione.

Na zvezdinu nesreću, gravitacija se ne zaustavlja na tome što je sabila zvezdu unutar horizonta događaja. Jačina gravitacije raste sve više dok čitava zvezda ne bude sabijena u jednu tačku. U toj tački pritisak i gustina su beskonačni, i što je još važnije zakrivljenost prostor vremena je beskonačna. To je tačka u koju ide zvezda. Svaki atom i svaka čestica zvezde potpuno su smrvljeni i uništeni na tom mestu. To je samo srce crne rupe, koje se zove singularitet.

Crna rupa je prazna, njena struktura je vrlo jednostavna. Crna rupa ima samo dva dela – singularitet i horizont događaja. Tu nema ničega. Nema atoma, nikakvih stena, ni gasova ni prašine. Ničega! Sva zvezdana materija je potpuno smrvljena i sabijena u singulartitet u centru crne rupe.

Mnogi čudni efekti OTR – isti oni koji su zanemarljivo mali na Zemlji, ili u blizini Sunca, višestruko su uvećani u blizini crne rupe. Usporavanje vremena, na primer, je na Zemlji potpuno zanemarljivo, ali na horizontu događaja koji okružuje crnu rupu vreme se potpuno zaustavlja. Prema našem svakodnevnom iskustvu znamo da se krećemo kroz prostor u tri pravca: gore-dole, levo-desno, napred-nazad, ali kroz vreme moramo da idemo samo u jednom smeru – od prošlosti ka budućnosti. Nasuprot tome, u crnoj rupi postoji sloboda kretanja kroz vreme, ali slobodu koju smo dobili u kretanju kroz vreme plaćamo zabranom kretanja kroz prostor. U crnoj rupi svi putevi pre ili kasnije vode u singularitet.

Crne rupe spadaju u najjednostavnije objekte u vasioni, ali to su najverovatnije i najčudniji objekti u našoj vasioni.

Zamislimo opet jednu masivnu zvezdu pred kraj njenog života. Pre početaka kolapsa prostor-vreme oko zvezde su neznatno zakrivljeni. Kako se zvezda sve više i više smanjuje, zakrivljenost prostor-vremena je sve veća i veća (slikovito gledano: na ravnom prostor vremenu nastaje sve veće i veće "udubljenje"). Ono šta se na kraju dešava sa ovim "udubljenjem" analizirali su Ajnštajn i Rozen tridesetih godina XX veka. Na njihovo iznenađenje našli su da se "udubljenje" opet otvara i povezuje sa drugom vasionom! Ovo neobično svojstvo crne rupe nazvano je Ajnštajn-Rozenov most. Ali to nije bilo sve. Kasnije se došlo do zaključka je moguće Ajnštajn-Rozenov most povezuje i dve udaljene tačke prostor-vremena naše vasione. Ovakvi “tuneli” nazivaju se crvotočine.

Treba napomenuti i to da crvotočine mogu da spajaju našu vasionu samu sa sobom na mnogo mesta, ali to bi bila različita mesta u prostor-vremenu. Drugim rečima, ulaskom u jednu od tih “drugih vasiona” mogli bi ponovo ući u našu vasionu, na istom mestu, ali u nekom drugom vremenu. To je mašina za putovanje kroz vreme. Teorijski, kad bi smo zaronili u rotirajući crvotočinu i pažljivo pilotirali našim vasionskim brodom mogli bi smo se ponovo pojaviti u našoj vasioni pre milijardu godina i posetiti Zemlju pre nego što su se na njoj pojavili dinosaurusi.

Bilo bi lepo koristiti ovakav vremeplov. Mogli bi da posetimo mnoge zanimljive događaje u prošlosti, uživo ih posmatramo ili čak u njima učestvujemo. Ali da li je ovakav vremeplov fizika ili naučna fantastika procenite sami.

* - * - *

Poslednjih dvadeset pet godina svog života Ajnštajn je proveo u traganju za Teorijom jedinstvenog polja, jednom teorijom koja bi opisala električna, magnetna i gravitaciona polja. On je 1953. godine, dve godine pre smrti, objavio rezultate svoje potrage za idealnom teorijom polja, dobijene do tog vremena. Verovao je da je uspeo da objedini fenomene gravitacije i elektromagnetizma u jedinstvenu teoriju. Na nesreću skup jednačina koje proizilaze iz njegove teorije daje beskonačan broj rešenja, a ne postoji način da se odredi koje rešenje je ispravno i važeće za našu vasionu. Da li je Ajnštajnova teorija jedinstvenog polja ispravna ili ne to još niko ne zna.