4. razred - Fizika

Dualna priroda čestica

Dualna (korpuskularno-talasna) priroda nije karakteristika samo svetlosti, odnosno elektromagnetnih talasa. Savremena fizika pokazuje da je dualnost univerzalna osobina svih objekata mikrosveta, dakle molekula, atoma i sitnijih čestica. U kvantnoj mehanici se i osobine makroskopskih tela (na primer kristala) kao kolektiva tih čestica objašnjavaju njihovom dualnom prirodom.

De Broljeva hipoteza

Svakoj čestici koja se kreće brzinom v i ima impuls p može se pridružiti talas talasne dužine:

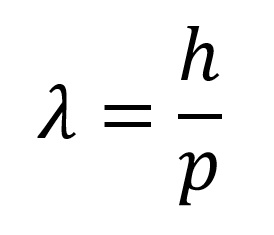
Prethodna relacija naziva se de Broljeva relacija. Talas pridružen čestici naziva se de Broljev talas a talasna dužina talasa koji je pridružen čestici naziva se de Broljeva talasna dužina. De Broljeva relacija važi za nerelativističke i za relativisticke čestice. Prethodna relacija se može napisati u obliku:

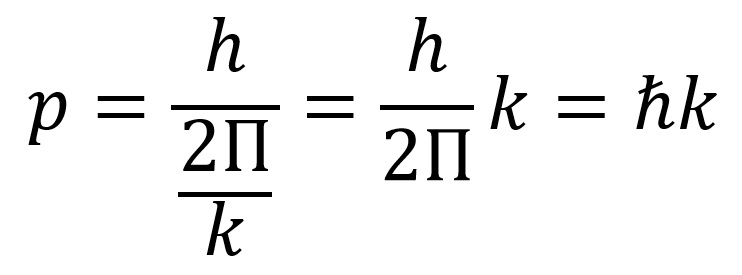
Odakle je talasni vektor de Broljevog talasa:

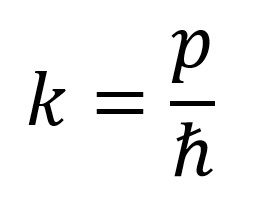
Gde je p impuls čestice. Kada je čestica kreće u polju neke sile (potencijalno polje) onda je njena ukupna energija jednaka:

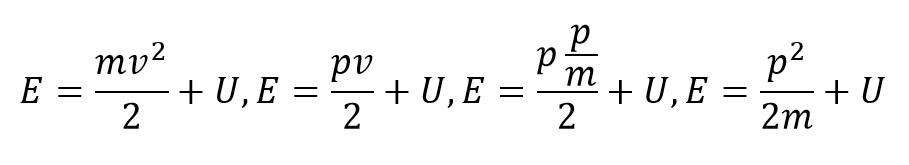
Čestica u polju neke sile naziva se neslobodna čestica, a čestica koja nije u polju sile naziva se slobodna čestica. Ako se kinetička energija izrazi preko impulsa čestice a potencijalna energija označi sa U, dobija se za ukupnu energiju neslobodne nerelativističke čestice:

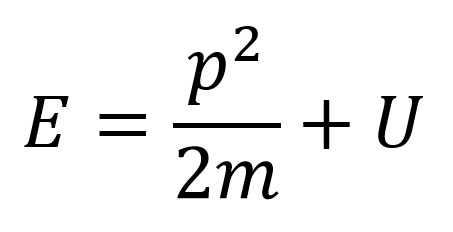
Na osnovu predhodne relacije i de Broljeve relacije izvesti formulu za talasnu dužinu talasa koji je pridružen neslobodnoj nerelativističkoj čestici.

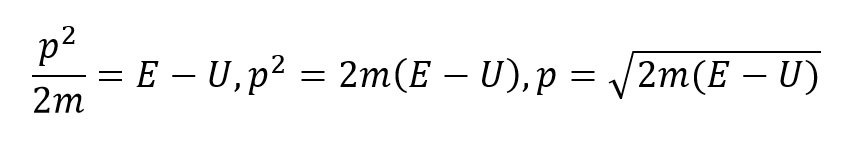
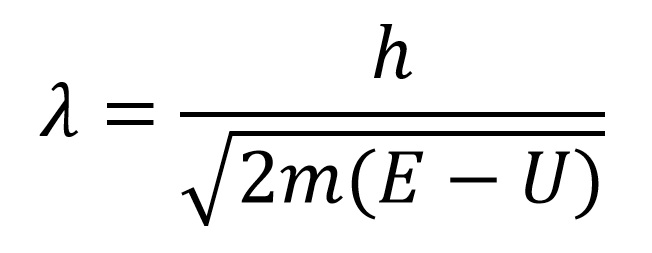
Ako je čestica slobodna onda je njena potencijalna energija jendaka nuli pa je de Broljeva talasna dužina slobodne čestice:

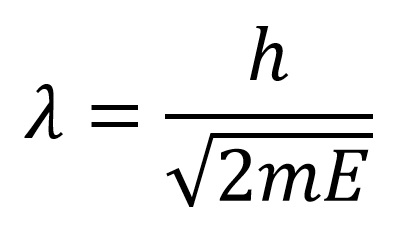
Gdje je E ukupna energija čestice koja je jednaka njenoj kinetičkoj energiji. Prema tome, ako se slobodna čestica kreće brže, njena kinetička energija je veća a de Broljeva talasna dužina je manja.

Ako postoje de Broljevi talasi onda se može registrovati i njihova difrakcija. Difrakcija se može registrovati pomoću difrakcione rešetke uz uslov de je njena konstanta reda veličine talasne dužine talasa koji stvaraju difrakcionu sliku. Zbog toga je potrebno odrediti red veličine de Broljevih talasnih dužina.

Difrakcija elektrona

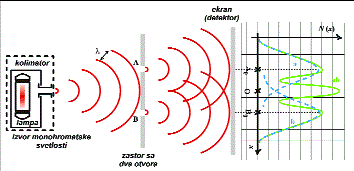
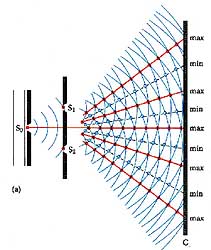
Difrakcija predstavlja pojavu prividnog skretanja talasa sa prvobitnog pravca prostiranja pri njegovom nailasku na ivice otvora ili na prepreku i tada se formiraju novi pravci prostiranja. Kada talas skreće sa pravca prostiranja i ulazi u oblast zaklonjenu preprekom u koji bez pojave skretanja zrak ne može da stigne, kaže se da talas zalazi u oblast geometrijske senke.

Pojava se objašnjava Hajgensovim principom. Do difrakcije dolazi kod prostiranja talasa svih vrsta elektromagnetnih (svetlost, H-zraka, radio talasa), zvučnih talsa itd. Osim toga difrakcija je potvrđena i kod fizičkih objekata na atomskom nivou, jer i čestice pokazuju talasne osobine i u ovom slučaju pojava se može objasniti principima kvantne mehanike. Iako do difrakcije dolazi kad god talas naiđe na prepreku, efekti difrakcije su najuočljiviji kada je veličina otvora (prepreke) reda veličine talasne dužine talasa. Najpovoljnija situacija za posmatranje difrakcije je kada talas nailazi na prepreku koja ima više bliskih otvora pomenutih dimenzija jer se tada na zaklonu formira difrakciono- interferenciona slika usled različitih putanja kojim se novonastali talasi prostiru.

Elektronski mikroskop

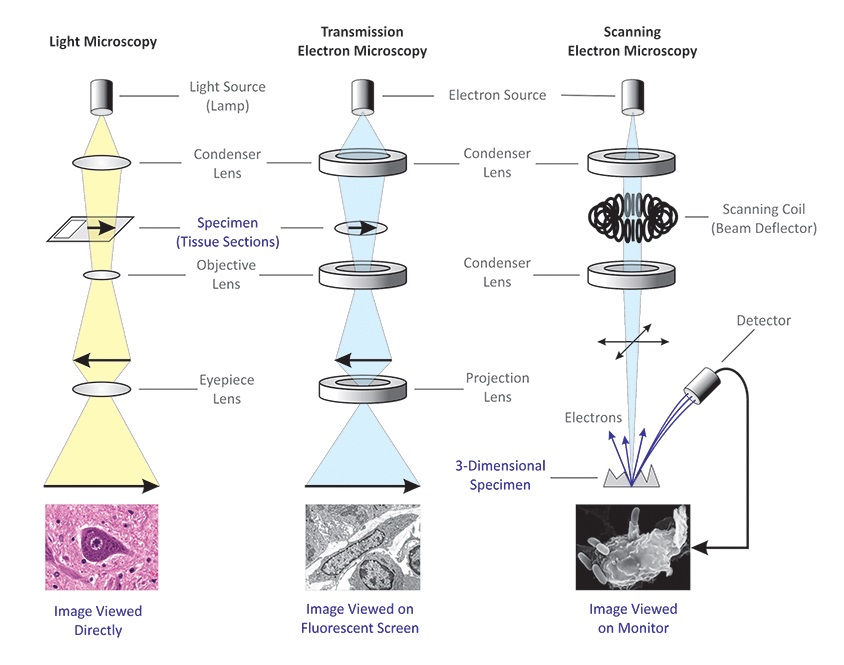
Elektronski mikroskop je izumljen u Nemačkoj 1932. godine, a širu je biološku namenu stekao tokom ranih pedesetih godina prošlog veka. Umesto vidljive svetlosti i optičkih sočiva, elektronski mikroskop koristi zrak elektrona, koji usmerava fokusirajući elektromagnetno polje. Iz razloga što je talasna dužina elektrona znatno kraća od one fotona vidljive svetlosti, granica rezolucije elektronskog mikroskopa je puno manja od svetlosnog mikroskopa: oko 0,1 - 0,2 nm elektronskog mikroskopa u poređenju sa oko 200 - 350 nm kod svetlosnog mikroskopa.

Međutim, za biološke uzorke stvarna granica rezolucije obično nije niža od 2 nm ili je viša, zbog problema sa pripremom preparata i kontrastom. Elektronski mikroskop ima oko 100 puta veću moć rezolucije od svetlosnog mikroskopa. Za posledicu je i iskoristivo povećanje takođe veće: do 100.000 puta elektronskog mikroskopa, u poređenju s 1.000 do 1.500 puta kod svetlosnog mikroskopa. Na taj način je, posmatrajući je elektronskim umjesto svetlosnim mikroskopom, moguće zapaziti mnogo više detalja u građi ćelije.

Poređenje mikroskopa:

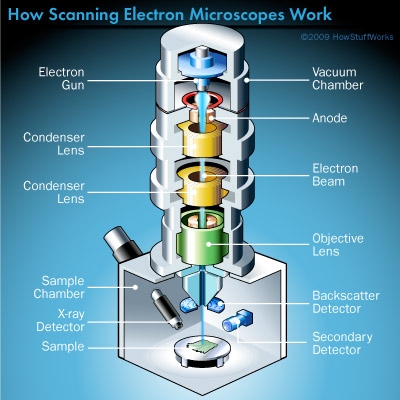
Princip rada elektronskog mikroskopa:

Ljudska kosa:

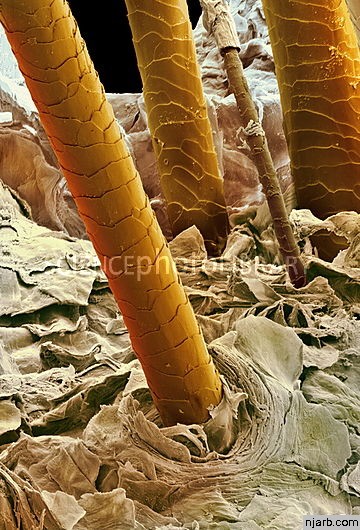
Crvena krvna zrnca:

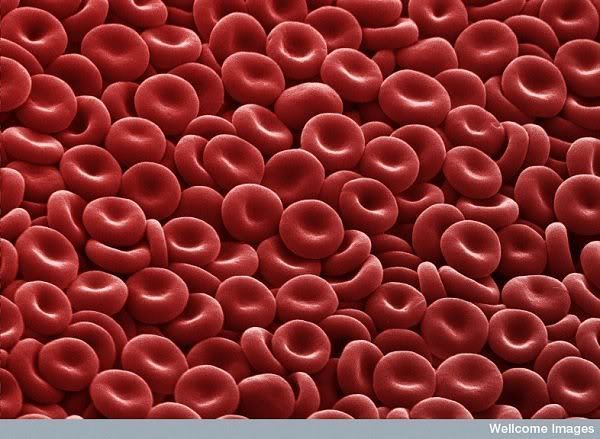
Hajzenbergova relacija neodređenosti

U kvantnoj mehanici, Hajzenbergov princip neodređenosti daje u obliku preciznih nejednakosti da određeni parovi fizičkih svojstava, kao što su pozicija i momenat, ne mogu da budu istovremeno poznati sa visokom preciznošću. Drugim rečima, što je preciznije jedno svojstvo izmereno, to se manje precizno drugo svojstvo može izmeriti.

Rezultat idealnog merenja u kvantnoj fizici je uvek karakterisan statističkom raspodelom. Standardna devijacija ove raspodele predstavlja neodređenost datog merenja i što je ona veća, to je veća i neodređenost. Klasična fizika pretpostavlja da je uvek moguće istovremeno meriti proizvoljan broj fizičkih veličina sa proizvoljno malim neodređenostima. Ova pretpostavka ne važi u kvantnoj fizici i u opštem slučaju takvo merenje više nije moguće te se stoga mora formulisati novi princip koji će dati vezu između neodređenosti istovremeno merenih veličina. Ovakav princip je istorijski prvi formulisao Verner Hajzenberg 1927. godine za položaj i impuls. Matematički formulisan on glasi:

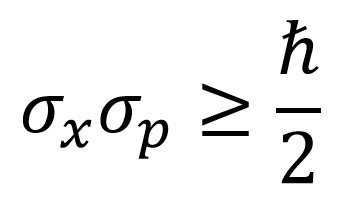
pri čemu je ℏ Dirakova konstanta, odnosno redukovana Plankova konstanta.

Šredingerova jednačina

Statistička tumačenja de Broljevih talasa i Hazenbergove relacije neodređenosti pokazala su da jednačina u kvantnoj mehanici koja opisuje mikročestice u polju sila, mora opisivati istovremeno i njena talasna svojstva. Prema tome, osnovu jednačine mora činiti talasna funkcija Ψ(x, y, z, t) ili veličina |Ψ|². Pošto tražena jednačina mora uzimati u obzir talasna svojstva čestice ona mora biti talasna jednačina slična jednačini koja opisuje elektromagnetne talase.

Osnovnu jednačinu nerelativističke kvantne mehanike je 1925. godine formulisao a 1926. godine objavio austrijski fizičar Ervin Šredinger. Kao i sve osnovne jednačine u u fizici (Njutnova jednačina u klasičnoj mehanici, Maksvelova jednačina za elektromagnetna polja), Šredingerova jednačina se ne izvodi već se postavlja a njenu ispravnost potvrđuju eksperimentalni rezultati.

Šredingerova jednačina se može izraziti na sledeći način:

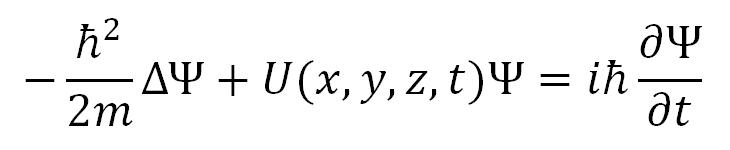
gde je m masa mikročestice, Δ Laplasov (Laplace) operator (ΔΨ = ∂²Ψ/∂x² + ∂²Ψ/∂y² + ∂²Ψ/∂z²), i je imaginarna jedinica a U(x, y, z, t) potencijalna energija čestice u polju sila u kome se ona kreće. Pošto se radi o nerelativističkoj Šredingerovoj jednačini, ona važi za bilo koju kvantnu česticu koja se kreće brzinom v mnogo manjom od brzine svetlosti c (v << c).

Ova jednačina predstavlja opšti oblik Šredingerove jednačine zavisne od vremena (Šredingerova nestacionarna jednačina) i ona je u matematičkom smislu parcijalna diferencijalna jednačina drugog reda.

Za mnoge pojave u mikrosvetu ova jednačina se može uprostiti ako se uzme da je talasna funkcija Ψ nezavisna od vremena. Ovo je moguće učiniti ako je polje u kojem se mikročestica kreće stacionarno, tojest funkcija U = U(x, y, z) ne zavisi od vremena i ima smisao potencijalne energije. Na taj način se dobija jednačina:

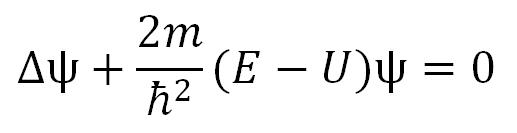
koja predstavlja Šredingerovu jednačinu za stacionarno polje i prosto se naziva Šredingerova jednačina.

U jednačini figuriše parametar ukupna energija čestice E. U teoriji diferencijalnih jednačina je pokazano da ova jednačina ima rešenje samo za određene vrednosti E. Ove vrednosti energije se nazivaju svojstvene vrednosti. Rešenja Šredingerove jednačine koja odgovaraju svojstvenim vrednostima energije nazivaju se svojstvene funkcije. Svojstvene vrednosti E mogu biti kako kontinualne tako i diskretne. U prvom slučaju se govori o neprekidnom ili kontinualnom spektru a u drugom slučaju o diskretnom ili linijskom spektru.

Ako se posmatra jednodimenzionalni slučaj, kada polje u kome se čestica kreće jednodimenzionalno, U(x), onda se prelazi na jednodimenzionalnu Šredingerovu jednačinu koja opisuje kretanje čestice duž jednog pravca:

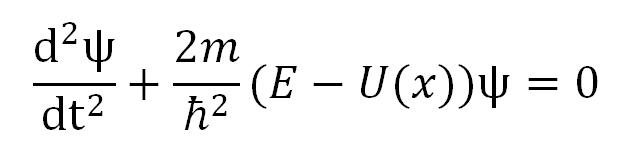
Za mnoge realne slučajeve oblik potencijalne energije ili nije poznat ili je jako komplikovan, tako da se ne može naći analitičko, već samo numeričko rešenje Šredingerove jednačine.

Kretanje slobodne čestice

Pri kretanju slobodne čestice, na koju nema uticaja polja, njena ukupna energija je jednaka kinetičkoj energiji. Ako se čestica kreće duž x-ose Šredingerova jednačina za stacionarno stanje ima oblik:

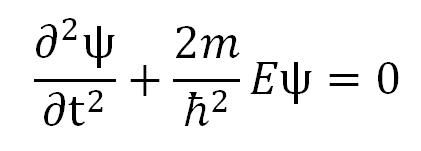
Rešenje je ψ(x) = Aexp(ikx) sa svojstvenom vrednošću energije E = ħ²k²/(2m). U ovom slučaju slobodna čestica može imati proizvoljne vrednosti energije, tojest energetski spektar je kontinualan.

Čestica u potencijalnoj jami beskonačne dubine

Ukoliko se posmatra jedan klasičan slučaj koji se odnosi na kuglicu u jami. Ukoliko se kuglica dovede do ruba jame i pusti, onda će se ona kretati unutar ove jame i ne postoji način da je ona napusti. Kaže se da je kuglica "zarobljena" u ovoj jami i da ona može da se kreće samo unutar nje. Ako bi se kuglici, dovedenoj na rub jame saopštila neka početna brzina onda bi ona ona mogla da napusti jamu. Očigledno da je u ovom slučaju klasične fizike kuglica i fizički (prostorno) i energetski zarobljena u jami.

U kvantnoj mehanici pod potencijalnom jamom se podrazumeva prostor u kome se mikročestica može slobodno kretati. Ovaj prostor je ograničen poljem koje ne dozvoljava mikročestici da ga napusti.

Jedan od idealizovanih slučaja, za koji je moguće naći analitičko rešenje Šredingerove jednačine, je kretanje čestice u potencijalnoj jami beskonačno visokih zidova, za koju potencijalna energija ima oblik:

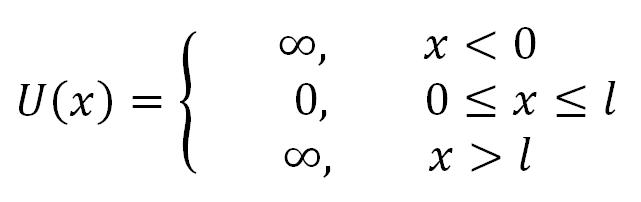
gde je l širina jame, a energija se računa od njenog dna. Pretpostavlja se da se mikročestica (elektron) kreće duž x-ose.

Šredingerova jednačina za ovaj jednodimenzionalni slučaj je:

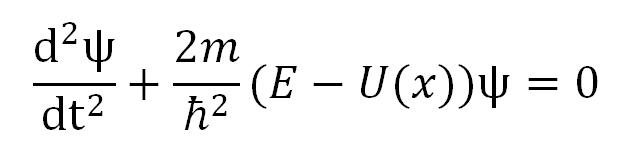
Iz uslova zadatka (beskonačno visoki zidovi) proizilazi da čestica ne može napustiti oblast jame. Prema tome verovatnoća nalaženja čestice (a time i talasna funkcija) za oblast van jame jednaka je nuli. Na granicama jame (pri x = 0 i x = l), zbog neprekidnosti talasne funkcije, vrednost Ψ jednaka je nuli. Dakle, granični uslovi u ovom slučaju su:

ψ(0) = ψ(l) = 0

U oblasti jame (0 ≤ x ≤ l) Šredingerova jednačina se svodi na jednačinu oblika:

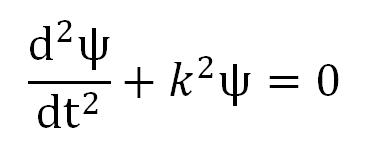
gde je k² = 2mE/ħ² . . (1)

Opšte rešenje diferencijalne jednačine može se napisati u sledećem obliku:

ψ(x) = Asin(kx) + Bcos(kx)

Iz uslova ψ(0) = 0 se dobija:

ψ(0)=0 sledi da je 0=Asin0+Bcos0=B iz čega se zaključuje da je B=0

Talasna funkcija koja je rešenje Šredingerove jednačine dobija oblik:

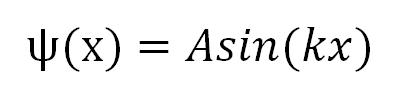
Uslov ψ(l) = A sin(kl) = 0 je ispunjen samo kada je kl = nΠ, gde je n ceo broj:

k = nΠ/l . . (2)

Iz izraza (1) i (2) sledi:

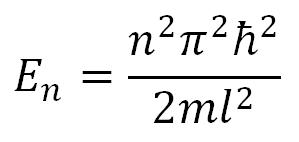
tojest da je Šredingerova jednačina, koja opisuje kretanje slobodne čestice u potencijalnoj jami sa beskonačno visokim zidovima, zadovoljena samo za svojstvene vrednosti E_n koje zavise od celog broja n. Prema tome, energija E čestice u potencijalnoj jami sa beskonačno visokim zidovima ne može biti proizvoljna, već ima diskretne vrednosti (kvantovana je). Kvantovana vrednost energije E_n naziva se energetski nivo, a broj n koji određuje energetski nivo naziva se kvantni broj. Ovo pokazuje da se mikročestica u potencijalnoj jami sa beskonačno visokim zidovima može nalaziti samo na određenim energetskim nivoima tojest u određenim kvantnim stanjima n.