2. osztály - Fizika
2. Termodinamika
Belső energia
Minden test függetlenül a halmazállapotától nagy számú részecskéből áll (atomok vagy molekulák).
Az atomok atommagból és elektronburokból állnak.
Az atommag kétféle nukleonból áll: proton és neutron.
Az elektronburokban az elektronok különböző pályákon köröznek az atommag körül.
Mindezek az atomot alkotó részecskék egymással kölcsönhatásban állnak:
* a mozgás által mozgási energiával rendelkeznek
* a kölcsönhatás által helyzeti energiával rendelkeznek
A testet alkotó részecskék össz mozgási és helyzeti energiája képezi a test belső energiáját.
A test belső energiaszámítása igen összetett, de egyes esetekben elfogatható hogy megegyezik az ideális gáz belső energiájával.
Az ideális gáz belső energiáját a részecskék káotikus hőmozgása képezi, mivel a részecskék nagy távolsaága végett a helyzeti energia eltekinthető.
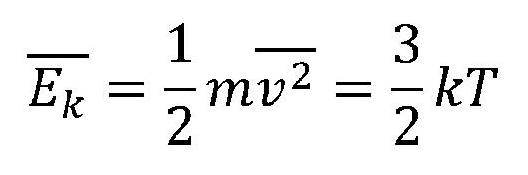
A tananyaghoz fűződő videófelvétel
Ha a gáz n számú részecskéből áll ezek belső összenergiája nyilván:
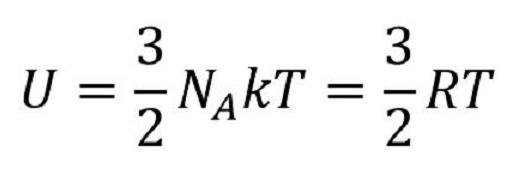
mivel: N=nNA a R=kNA,
NA=6.022.1023 [mol-1] - Avogadro szám
k=1.38.10-23 [J/K] - Boltzmann állandó
R=8.313 [J/molK] - univerzális gázállandó
n - mólok száma
A belső energia mértékegysége Joule, mint bármelyik más energiaesetében.
A belső energia változása
Minden test nagy számú részecskéből áll, ennek következménye hogy a testek a belső energiájuk is nagy. Az ideális rendszer belső energia változása csak a hőmérséklet kezdő és végső érték különbözetétől függ.
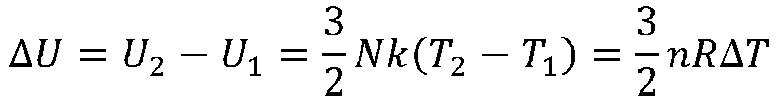
A test belső energiája megváltozhat a környezettel folytatott hőcsere (hőátadás) következetében vagy mechanikai munka végzése által.
Előfordulhat hogy mindkét folyamat közrejátszik egyidejűleg.
A belső energia változása mechanikai munka által: egy szögre ha kalapáccsal többször ütünk, a szög is meg a kalapács is melegedni fog; biciklikerék pumpálása alatt a pumpa melegedni fog.
A mechanikai munkán kívül hőcserével is változhat a test eneriája érintkezés által. A melegebb test érintkezés által veszíti a hőmérsékletét amíg a hozzáérintkező hidegebb test melegedni fog.
A hőmennyiség
Amikor két különböző hőmérsékletű test kontaktusban van, közöttük hőcsere történik. A hőcsere addig tart amíg a két test hőmérséklete nem lesz egyforma.
A hőmennyiség fogalma bevezetése lehetővé tette a hőcsere által a belsőenergia változások meghatározását.
A testek hőcsere által történő belsőenergia változások mértéke a hőmennyiség
A hőmennyiség melyet egy test átad vagy átvesz, a test tömegétől, hőtani sajátosságaitól és a hőmérséklet változásától függ.
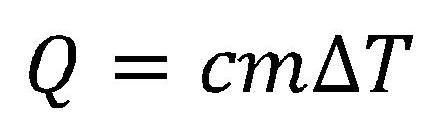
A képletben:
- Q - hőmennyiség
- c - fajhő
- m - tömeg
- ΔT - hőmérséklet változása
Termodinamika első főtétele
A termodinamika első főtétele a termodinamikai rendszerekre kimondja az
energiamegmaradást, vagyis azt, hogy az energia a termodinamikai
folyamatok során átalakulhat, de nem keletkezhet és nem veszhet el.
Röviden:
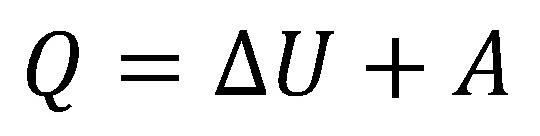
A rendszerrel közölt hő növelheti a rendszer belső energiáját, vagy
munkát végezhet.
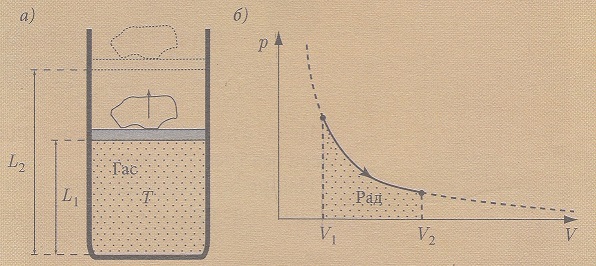
Egy edényben amely mozgó dugattyúval van ellátva ideális gáz van. A dugattyún egy kő (súly) van elhelyezve. A dugattyúnak a súrlódása elhanyagolható. A rendszernek egy külső forrás hőt ad át. A rendszernek leadott hő által a belső energiája növekszik és a rendszer munkát is végez. Az ideális gáz részecskéi a hőmérséklet által gyorsabban mozognak és nyomást végeznek az edény falaira, valamint a dugattyúra amely a kővel magasabbra emelkedik. Ebben az esetben az ideális gáz belső energiája növekedni fog (a hőmérséklet növekedése által) és a rendszer munkát is fog végezni (a dugattyú és a kő helyzeti energiája növekedni fog, ezáltal egy meghatározott munka lesz elvégezve).
A képlet rövid elemzése (mi történik ha valamelyik érték nulla):
a) Q = 0 - a rendszert nézve nincs hőhozzáadás sem elvétel, akkor a A = -ΔU a munka csak a belső energia alapján történik, és a rendszer belső energiája emiatt csökken.
b) ΔU = 0 - a rendszer belső energiája nem változik akkor a Q = A - a rendszernek átadott összes energia a munkát végzi. Ez az izoterm folyamat.
c) A = 0 - a rendszer nem végez munkát. Akkor a Q = ΔU illetve a rendszernek átadott hő a rendszer belő energiáját növeli. Ez izochór folyamat.
Az izofolyamatok:
* izoterm (állandó hőmérséklet),
* izochor (állandó térfogat),
* izobár (állandó nyomás).
Az elhangzottak alapján az a következmény hogy: lehetetlen megépíteni perpetuum mobile-t, örökmozgó gépet, mely magától fog dolgozni, befektetett energia nélkül.
A gáz munkája
Képzeljük el hogy az ideális gáz hengerben van amelynek a dugattyúja mozogni tud le és fel súrlódás nélkül. Az izobár munka mely a gáz terjedésén alapul, illetve a nyomás ereje mellyel a gáz a dugattyura hat: F = p * S az erő egyenlő a nyomás és a dugattyú felülete (melyre a gáz részecskéi nyomással hatnak) szorzatával.
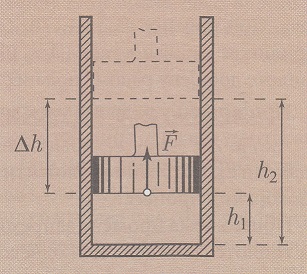
Az erő hatása által a dugattyú el fog mozdulni egy bizonyos távolságra:
Δh = h2 - h1
Ilyen feltételeknél a munka amely gáz nyomás végez, a gáz tágulása
végett:
A = F * Δh = p * S * (h2 - h1)
Illetve így is lehet írni:
A = p * ΔV
a ΔV - a gáz térfogatváltozása.
Táguláskor a munka pozitív mert a gáz kifejtette erő iránya azonos
a dugattyú elmozdulásának irányával. A tágulás során a gáz a dugattyú
közvetítésével energiát közöl környezetével.
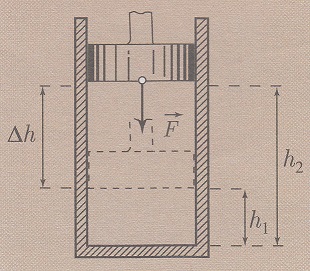
A gáz összenyomásakor a levezetett képletek érvényesek, de mivel a V2 < V1, a munka negatív lessz. A gáz munkája és a külső erők munkája a dugattyú azonos elmozdulásakor egyenlő nagyságú, csak az előjelben különbozik: A’ = -A = - p * ΔV
Izoterm, izobár és izochor állapotváltozások
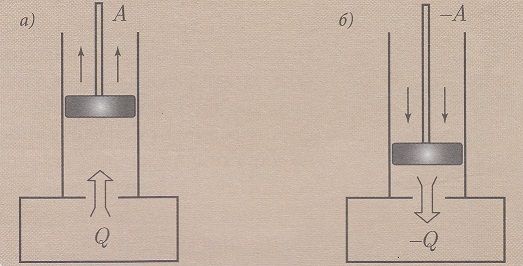
Az izoterm állapotváltozást a Boyle-Mariotte törvény írja le. Izoterm állapotváltozásnál a gáz belső energiája nem változik mivel a hőmérséklet állandó.
ΔT = const ebből kifolyólag ΔU = 0.
Az előbbit figyelembe véve és a a termodinamika első főtétele alapján következik: Q = A = p * ΔV
A gázzal izoterm módon közölt hő teljes egészében a gáz tágulási munkájára fordítódik.
Az a) ábrán a gáz a hengerben hőt vesz fel és tágul (a munka pozitív).
A b) ábrán hőelvonás történik, minek következtében a gáz térfogata csökken (a munka negatív).
A fentiekből kitűnik hogy a munka és a hőmennyiség előjele azonos. Táguláskor (A>0) a rendszer bizonyos hőmennyiséget kap (Q>0).
Az izoterm folyamatokban a gáz belső energiája alakul munkává és viszont.
Az izochor állapotváltozást a Charles törvénye írja le. Mivel ebben az esetben a térfogat állandó a gáz munkája nulla lessz. Az össz hőmennyiség amelyet a gáz fölvett a belső energiát növeli.
Izobár változás esetén Gay-Lussac törvény érvényes, és a gáz
munkáját az állandó nyomás és a térfogatváltozás adja:
következik: A = p * (V - V0) = p * ΔV
ahol V0 a kezdő a V a végső térfogat.
A gázok hőkapacitása és fajhője
A szilárd és cseppfolyós halmazállapot esetén a kisebb hőmérséklet változások nem okoznak jelentősebb hőtágulásokat, illetve a hőtágulás által végzett munkát nem kell figyelembe venni (A= 0). A gázoknál létezik:
- állandó nyomás mellet mért fajhő
- állandó térfogat mellet mért fajhő.
Ezeket a különbségeket a gázoknál nem lehet figyelmen kívül hagyni.
Amennyiben bizonyos hőmennyiség van átadva a gáznak állandó térfogat megtartásánál, az a hő csak a belső energia novekedését idézi elő.
Amennyiben bizonyos hőmennyiség van átadva gáznak állandó nyomás megtartásánál, az a hő által növekszik a belső energia és munka végződik.
A gáz mólhője állandó térfogat mellett (CV) az a hőmennyiség amely az egy mól mennyiségű gáz hőmérsékletét egy Kelvin fokkal megváltoztatja.
A gáz mólhője állandó nyomás mellett (CP) az a hőmennyiség amely az egy mól mennyiségű gáz hőmérsékletét egy Kelvin fokkal megváltoztatja.
A CP/CV arány jelölése k, és különböző értéke van az egyatomos, kétatomos, háromatomos, ... molekulák esetében.
Egyatomos molekulák k = 1.67
Kétatomos molekulák k = 1.40
Három és többatomos molekulák k = 1.33
------------------
CP = 5R/2
CV = 3R/2
CP - CV = R
Adiabatikus állapotváltozás
A folyamat mely a gáz és a környezete (külső testek) között hőcsere nélkül történik adiabatikus állapotváltozásnak nevezik.
Az egyik módja hogy a gáz tökéletesen hőszigetelt tartályban legyen, a második módja hogy az állapotvátozás olyan gyors legyen hogy ne történjen hőcsere a környezettel.
A gyakorlatban nem létezik tökéletes hőszigetelés és a folyamatok is időigényesek, illetve a valóságos folyamatok csak megközelítőleg adiabatikusok.
A folyamat adiabatikus jelleme a következő képlettel van kimutatva: Q = 0, a termodinamika első főtétele alapján Q = ΔU + A következik hogy az adiabatikus folyamatknál: ΔU = -A vagy A = -ΔU. Az adiabatikus folyamatoknál a munka és a belső energia előjelei ellentétesek. Adiabatikus terjedésnél a gáz hül, amíg az adiabatikus osszenyomásnál a gáz melegszik.
Boyle-Mariotte törvény alapján pV = const.,
amíg az adiabatikus folyamatnál pVk = const. amíg a k = CP/CV - Poisson száma
Visszafordítható és visszafordíthatatlan folyamatok
A mechanikai munka végzésére léteznek természetes energiaforrások (ember és állat izmai, levegő és víz mozgása).
A korszerű társadalom szüksékleteire (autók, hajók, vonatok, repülők meghajtására) más energiaforrásokat alkalmaznak. A molekulák helyzeti energiáját mozgási energiává változtatják (illetve belső energia és hő az ami ebből kapható).
Az így megkapott mozgási energia tovább átalakítható más fajta energiába vagy megint hővé (illetve belső energiává). Ebből kifolyólag lehetséges hogy a természetben a folyamatok visszafordíthatók.
A tapasztalat azt mutatja hogy az energia csak részben alakul át mechanikai munkává és az állapot visszafordíthatatlan a vesztességek megjelenése a folyamat során.
Minden termodinamikai folyamat visszafordíthatatlan energiai szempontból mivel nem létezik tökéletes gép mely veszteség nélkül működne (pl. súrlódás vagy levegőellenállás). A belső égésű motoroknál ezek a vesztességeket üzemanyag fogyasztással vannak pótolva.
Az entrópia
Ezt a foglamat Német fizikus Rudolf Julius Emanuel Klauzijus vezette be termodinamikai jelenségek és problémák megoldása során.
A test (rendszer) belső energia átalakítása más energiává jobbnak mutatkozik (kevesebb veszteséggel), amennyiben a hőmérséklete magosabb a környezetében található testekhez viszonyítva. Másrészt gyakorlatilag lehetetlen a test (rendszer) belső eneriáját átalakítani amennyiben a hőmérséklete nem sokkal eltérő a környező testekhez viszonyítva, különösen ha az alacsony hőmérsékletekről van szó.
Minden folyamatnál, hőjelenségnél jellegzetes a hőmennyiség amely hőcsere által a termodinamikai rendszerek, vagy a rendszerek és a környezetük között történik.
A hőmennyiség a hőfolyamatot jellemzi, nem a termodinamikai állapotot. A rendszer (test) hőmérséklet növelése bizonyos hőmennyiség átvétele által a részecskék káotikus mozgását noveli, amivel a rendszer rendetlensége növekszik. A rendszer rendetlenségét nem csak az átvett hő határozza, hanem a hőmérséklet is melyen az adott folyamat történik. Magosabb hőmérsékleteken a részecskék rendetlenebb mozgása nagyobb és a rendszernek közölt hő kisebb hatással van a renszer rendetlenségére.
Ez a tény vezette rá fizikusokat hogy a leírt hiányosságot megmagyarázzák és definiálják a hőmennyiség és a hőmérséklet által. Ez a redukált hőmennyiség illetve entrópia:
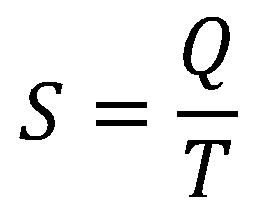
Mértékegysége Joule per Kelvin J/K.
Entrópia is mintahogy a belső energia a rendszer állapotának a fügvénye. Kizárólag a rendszer paramétereitől függ, melyek a rendszer állapotát írják le. Csak az entrópia változásának van gyakorlati jelentősége.
Minden valós termodinamikai folyamat energiavesztességel jár. Mindezek a folyamatok kisebb vagy nagyobb mértékben visszafordíthatatlanok és az entrópia növekedése jellemzi őket.
Minden valós folyamatot amely zárt rendszerben történik entrópia növekedése jellemzi.
Entrópia a rendszer törekvése hogy a nagyobb rendetlenség felé haladjon. A rendszer legrendezettebb az abszolút nulla fokon.
Termodinamika második főtétele
Tapasztalatból ismert jelenség hogy a hő magától a melegebb testről a hidegebb tesre megy át. A termodinamika első főtétele nem lenne felborítva ha a hő a hidegebb testről a melegebbre térne át, ha a zárt rendszer energiája nem változna e folyamatnál. A tapasztalat még nem mutatott ilyan spontán jelenséget.
A termodinamika első főtétele engedélyezi a teljes mozgási energia átalakulását belső energiává (mintahogy a test belső energia átalkulását mozgási energiává).
Termodinamika második főtétele meghatározza a hőfolyamatok irányát.
Többféleképpen definiálható a termodinamika második főtétele, például:
A hő magától csak a melegebb testekről megy át a hidegebb testekre, fordítva a hő átmenetele a hidegebb testekről a melegebbekre nem történik magától (spontánul).
Hőerőgépek
A mai életet nehéz lenne elképzelni hőerőgépek nélkül. A hőerőgépek a szerkezetüktől függetlenül valamilyen munkavégző közeg belső energiáját átalakítják a mechanizmusok energiájévá. Az energiaátalakítás során egyidjűleg hőcsere folyik különböző hőmérsékletű testek között, miközben a munkavégző közeg (gőz vagy gáz) a nyomás révén munkát végez. Ahhoz hogy ez végbemehessen, az üzemanyag (szén, benzin, gáz, stb.) át kell hogy adja égéshőjét a munkavégző közegnek.
Jelentős a gőzturbinák alkalmazása a hőerőművekben a generátorok működésénél. A gőzturbinákat az atomerőműveknél is használják ahol a magashőmérsékltű gőz előállításához a nukleáris folyamatokat alkalmazzák.
A korszerű közlekedés valamenyi hőerőgép fajtáján alapszik. Az autókban, traktotokban, kombájnokban belső égésű motorokat használnak. A repülőgépek meghajtásánál gázturbinákat használnak. A reaktív motorok ugyanúgy a hőerőgép elveken alapszanak és az űrrakétáknál alkalmazzák.
A hőerőgép energiamérlege és működési elve
A hőerőgépek olyan berendezések melyekben a belső energiából mechanikai erő kapható.
Minden hőerőgép a belső energia átalakítása során hőt ad le a környezetének.
Minden hőerőgép három részből áll:
- munkavégző közeg,
- melegítő és
- hűtő.
A hűtő keggyarabban a légkör, víz de a fold is olykor szerepel mint hűtőtest.
A munkavégző közeg leginkább gáz vagy gőz zárt edényben mozgó dugattyúval.
A munkavégző közeg a melegítőtől hőt vesz föl. A munkavégzés után, miközben a munkavégző közeg összenyomódik bizonyos hőt ad le (a melegítőnél sokkal alacsonyabb hőmérsékletű) a hűtőnek. A gáz terjedése idézi elő a dugattyú elmozdulását a motor hengerében. A gáz terjedése alatt a nyomása csökken, amíg nem lessz egyforma a külső nyomással. Akkor a terjedés leáll és a gáz a hengerben leáll a munka végzésével. Ezután szükséges a gázt összenyomni a kezdő állapotba, melyet külső erő tesz lehetővé. Így történik a időszakosan a gáz terjedése és összenyomása.
Hatásfok
A termodinamikai ciklusoknak szükséges meghatározni az energiamérlegét. A ciklus hatásfoka a megkapott és a befektetett munka aránya.
η = A/Q1 = (Q1-Q2)/Q1
A hatásfok értéke nagyobb nullától és kisebb egynél. A hatásfok értéke nem lehet egy, mivel minden folyamatnál hőveszteség jelentkezik.
Hozzávetőleges hatásfok értékek:
Gőzgép: 8%
Emberi test: 25%
Benzin motor: 25%
Dízel motor: 36%
Vízturbina: 80%
Elektromotor: 85%
Transzformátor: 98%