2. osztály - Fizika
3. A fluídumok dinamikája
A fluídumok áramlása
Fluidum latin szó, nem szilárd halmazállapotra vonatkozik, "önthetőek". Közös tulajdonságuk a részecskék szabad mozgékonysága. Dinamikájukat az ideális fluidum modelljén tanulmányozzák (függ a nyomástól, sűrűségtől, hőmérséklettől, áramlás sebességétől). Mozgásuk az úgynevezett STACIONÁRIUS ÁRAMLÁS (áramlási tér pontjaiban a részecskék sebessége nem változik az időben). A gáz, mint fluidum összenyomható, részecskéik között nincs súrlódás.
A kontinuitás egyenlet
A kontinuitási egyenlet a tömegmegmaradás alkalmazása a fluidum áramlására. Az összenyomhatatlan fluidum stacionárius áramlása esetén az áramlási cső keresztmetszetének és a hozzá tartozó áramlási sebességének a szorzata állandó. Ahol kiszélesedik az áramlási cső, ott lelassul az áramlás, ahol pedig összeszűkül a cső ott felgyorsul az áramlás. Példa a locsolócső összenyomása. A kontinuitási egyenlet jelentős az ipar és a műszaki gyakorlat szempontjából.
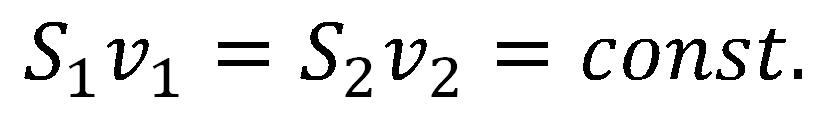
A képletben:
- S1 i S2 - keresztmetszet
- v1 i v2 - a fluídum áramlási sebessége

A Bernoulli egyenlete
Ez az egyenlet az energiamegmaradás törvényének az alkalmazása a fluidumáramlásra. Az áramlási cső bármely keresztmetszeténél egyenletes az áramlási sebesség.
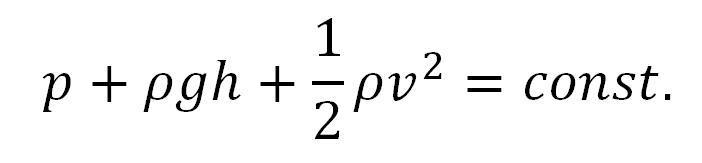
A nyomás három fajtája:
- p - statikus nyomás
- ρ*g*h - magossági nyomás
- 1/2*ρ*v2 - dimanikus nyomás
Minnél nagyobb egy keresztmetszetnél a fluidum statikus nyomása, annál lassabban áramlik és forditva.
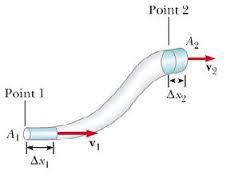
A Bernoulli egyenlet alkalmazása - Torricelli tétel
A vízzel teli hordóból egy kis nyíláson áramlik a folyadék. Ha a nyílás a hordó méreteihez képest kicsiny, akkor a hordóban a folyadékszínt megközelítőleg állandónak vehető.
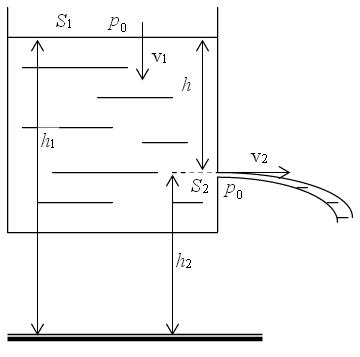
Bernoulli egyenlet: p + 1/2*ρ*v2 + ρ*g*h = const.
A Bernoulli egyenlet alkalmazása ezen a példán:
p0 + 1/2ρv22 + ρgh2 = p0 + 1/2ρv12 + ρgh1 (p0 és p0 törlik egymást):
1/2ρv22 + ρgh2 = 1/2ρv12 + ρgh1 Az egyenletet elosztani ρ-val:
1/2v22 + gh2 = 1/2v12 + gh1 Amennyiben a v22 lesz kifejezve:
v22 = v12 + 2gh1 - 2gh2 2h a zárójel előtt:
v22 = v12 + 2g(h1 - h2) A képről h = h1 - h2 :
v22 = v12 + 2gh
A képről és a kontinuitási egyenlet alapján leírható: S1v1 = S2v2
Mivel: S1 >> S2 meg lehet állapítani hogy v2 >> v1 illetve v1 ≈ 0 a folyadék színt állandó.
Ez alapján: v22 = 2gh illetve v2 = √(2gh)
A Bernoulli egyenlet alkalmazása - Pitot cső
A fluidumáramlást erősségét méri. A legegyszerűbb eset egy nyitott csatornában lévő folyadék áramlásának mérése.:
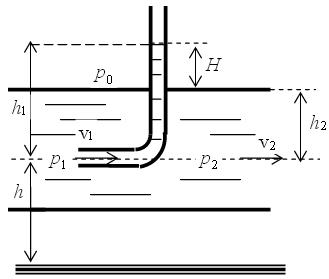
Bernoulli egyenlet: p + 1/2*ρ*v2 + ρ*g*h = const.
A Bernoulli egyenlet alkalmazása ezen a példán:
p2 + 1/2ρv22 + ρgh2 = p1 + 1/2ρv12 + ρgh1 a pipa bemenetén a folyadék nem mozog, illetve v1 = 0 a statikus és abszolút nyomások az adott pontokban:
p1 = p0 + ρgh1 és p2 = p0 + ρgh2 a v1, p1 és p2 beillesztésével:
p0 + ρgh2 + 1/2ρv22 + ρgh2 = p0 + ρgh1 + ρgh1
a v2 tag kifejezve
1/2ρv22 = p0 + ρgh1 + ρgh1 - p0 - ρgh2 - ρgh2 +p0 és -p0 eltűnnek,
1/2ρv22 = ρgh1 + ρgh1 - ρgh2 - ρgh2 az egyenlet elosztva ρ-val:
1/2v22 = gh1 + gh1 - gh2 - gh2 a tagok összeadása:
1/2v22 = 2gh1 - 2gh2 2g a zárójel előtt:
1/2v22 = 2g(h1 - h2) a képről H = h1 - h2:
1/2v22 = 2gH illetve: v2 = √(2gH)