2. osztály - Fizika
5. Elektrosztatika
Elektromos töltésű testek kölcsönhatása
Az atom magból és atomhéjból áll. Az atommag protonokból (pozitív töltésűek) és neutronokból (semleges töltésűek) áll, amit nukleonnak nevezünk. Az atomhéj negatív töltésű elektronokból áll. A proton és az elektron töltése azonos nagyságú, de ellentétes előjelű.
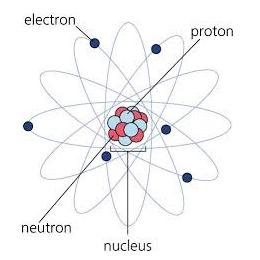
Ha egy test elektromosan semleges, az azt jelenti, hogy benne a protonok és az elektornok száma megegyező. Egy test akkor válik negatív töltésűvé, ha elektrontöbblete van. A pozitív töltésű test elektronhiányt szenved.
A szilárd anyagokban (különösen a fémekben) mindig vannak úgynevezett szabad elektronok. Általában az atom legkülső elektronjai szabadulnak el, ezeket az atommag gyengébben köti, ezért szabad elektronoknak tekintjük őket. A testek „megelektromozása” történhet érintéssel vagy dörzsöléssel, és ilyenkor mindig a szabad elektronok jutnak az egyik testről a másikra. Az, hogy melyik test adja le (pozitív töltésűvé válik) és melyik veszi fel (negatív töltésűvé válik) az elektronokat, az anyagok természetétől függ.
A töltésmennyiség
A töltésmennyiség az elektronok többlete vagy hiánya egy testben, a semleges állapothoz viszonyítva, amikor az elektronok és a protonok száma megegyezik. A test elektromos töltésmennyisége a test elektromos állapotának a mértéke. Az elektromos töltés az elemi töltés egész számú többszöröse:
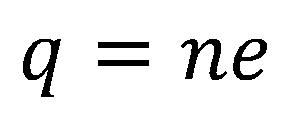
A képletben:
- q - a töltésmennyiség [C],
- n - az elektronok száma,
- e - az elemi töltés [C].
Az elektromos töltés mértékegysége a coulomb (ejtsd: kulon), rövidítve: C és az 1C = 6,24 * 1018e
Az elemi töltés coulomb-ban kifejezve: e = 1,620 * 10-19 C
Az elektromos erő. Coulomb törvénye
A viszonylagos nyugalomban lévő pontszerű töltések között ható elektrosztatikus erő törvényét Coulomb francia fizikus fedezte fel 1785-ben. Coulomb törvénye a következőképpen hangzik:
A két nyugvó pontszerű vagy gömb alakú töltés között ható elektrosztatikus erő egyenesen arányos a töltések szorzatával, és fordítottan arányos a közöttük lévő távolság négyzetével.
Az erő hatásvonala a töltéseket összekötő egyenes szakaszon van, és mindkét töltésre ugyanakkora, csak ellentétes irányú erő hat (akció-reakció):
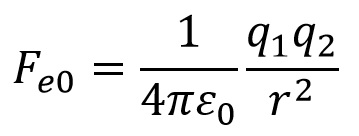
A képletben:
- ε0 – a vákúum dielektrikus permitivitása, melynek az értéke ε0 = 8,85*10-12 C2/Nm2
- q1 i q2 - az adott testek töltésmennyisége
- r - a testek közötti távolság.
Az erő vonzó lessz amennyiben a testek töltése ellentétes (az egyik pozitív a másik negatív töltésű). Az erő taszító lessz amennyiben a töltések egyforma előjelűek (mindkét test töltése pozitív, vagy mindkét test negatív töltésű).
A gravitációs erőkkel ellentétben az elektromos erők nagyon függenek a közegtől is melyben a testek vannak. A relatív permitivitás ε egy nevezetlen szám, amely megmutatja, hogy e bizonyos közeg a vákuumhoz képest hányszor csökkenti az elektrosztatikus erő értékét. A relatív permitivitás az anyagok tulajdonsága.
ε = ε0 * εr
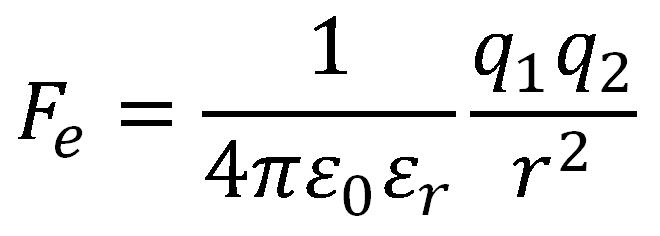
Az elektromos mező
Ahogy minden testet körülvesz egy gravitációs mező, ugyanúgy a nyugvó töltéseket is körülveszi egy elektromos (elektrosztatikus) mező. Az elektromos mező közvetíti az erőt a másik töltéshez, ha az elektromos mező „forrását” képző töltés közelébe kerül. Az elektromos erő lehet pozitív vagy negatív.
Az elektromos mező, a gravitációs mezőhöz hasonlóan kitölti a teret a test körül, és ez specifikus fizikai változásokat okoz. Az elektromos mezőnél a töltés a meghatározó tényező, míg a gravitációs mezőnél a tömeg.
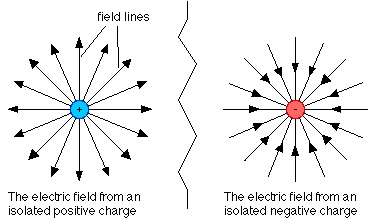
Az elektromos mező ábrázolására erővonalak szolgálnak. Az erővonalak konvencionálisan (megegyezés alapján) a pozitív töltésből erednek, és a negatívba torkollanak.
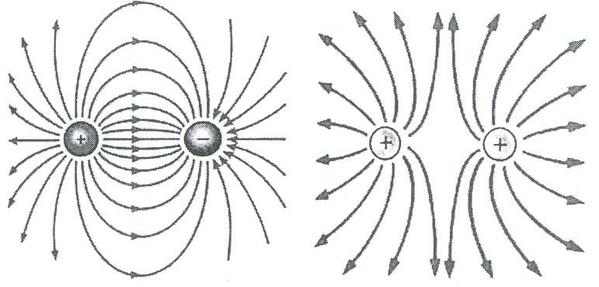
Az elektromos mezőt a gravitációs mezőhöz hasonlóan két fizikai mennyiség jellemzi: az elektromos térerősség és az elektromos mező potenciálja.
Az elektromos térerősség
Az elektromos térerősség fizikai érték mely egyenlő az elektromos erő és a töltésmennyiség hányadosával. Az elektromos térerő vektoriális érték.

Az elektromos térerő értéke:
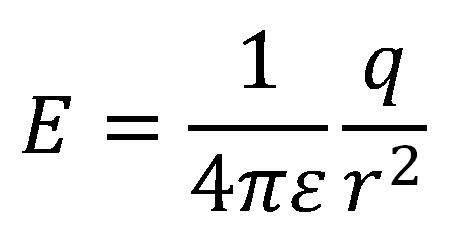
Az elektromos térerősség és az elektromos potenciál
Az elektromos térerősség a közegtől függ melyben a töltések találhatók. Arányos a testek töltésmennyiségeivel és csökken a testek taávolsága növekedésével.
Az elektromos munka és az elektromos feszültség
Amennyiben egy q próbatöltés az elektromos térerősség hatássára elmozdul egyik pontból a másikba, bizonyos munka lesz elvégezve.
Egy "Q" töltésű test elektromos mezőjének a potenciálja az "r" pontban a vákúumban:
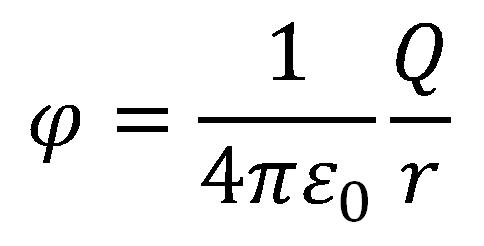
Az elektromos potenciált kis Görog φ (fi) betűvel jelölik.
Az elektromos potenciál mértékegysége volt 1V = 1J/1C.
Az elektromos mező két pontja közötti feszültség a két pont potenciáljának a különbsége.
U = φ2 - φ1
Ugyanúgy, az elektromos mező két pontja közötti feszültség megegyezik e elektromos mező munkájával egy pozitív próbatöltés áthelyezésével a mező egyik pontjából a másikba.
Az elektromos fluxus
A gömbalakú töltés térerő vonalai ha más töltés nem található a közelben egyenletesen terjednek sugarakként. A pozitív töltésnél a sugarak a testből erednek amíg a negatív töltés esetében ellentétesen.
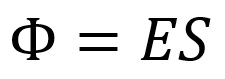
Az elektromos fluxus egyenlő a vonalak számával melyek a merőlegesen helyezett síkon haladnak át. Ahol a vonalak sűrűbbek az elektromos erő is nagyobb. Az elektromos fluxust meg lehet határozni az elektromos térerő (E) és az (S) terület alapján. A terület (S) a térerővel merőlegesen elhelyezett síkon található.
Ekvipotenciális síkok
Az elektromos térerő csökken a töltéstől (amelyből ered a térerő) távolodva. Minden pont a térben melynek egyforma a potenciálértéke egy ekvipotenciális síkot ábrázol.
Jačina i potencijal električnog polja
Rad elektirčnih sila izražava se na dva načina: preko jačine polja i razlike potencijala među tačkama polja. Uzimajući to u obzir, između jačine polja i njegovog potencijala postoji odgovarajuća veza.
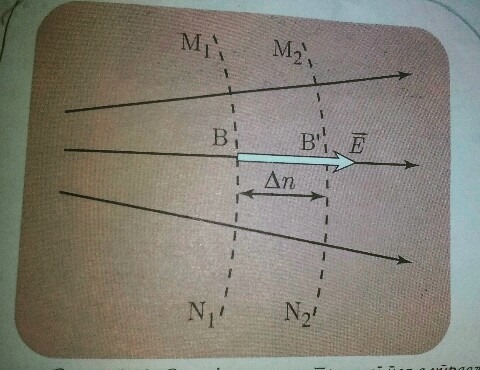
Smer jačine električnog polja upravljen je u stranu smanjivanja potencijala.
Imamo i formulu E= -∆V/∆n
Na osnovu izvedene veze između jačine i potencijala električnog polja, jednostavno je definisati jedinicu jačine polja. To je volt po metru: [E]= V/m.
Električna kapacitivnost
Fizička veličina kojom se karakteriše svojstvo provodnika da pri istom potencijalu mogu da sadrže različite količine naelektrisanja naziva se električna kapacitivnost.
q = CV
Električna kapacitivnost tela brojno je jednaka odnosu količine naelektrisanja tela i njegovog potencijala. Jedinica električne kapacitivnosti je farad (F): F = C/V
Električni kondenzator
Energija elektrostatičkog polja
Naelektrisanje provodnika i odgovarajući potencijal vezani su relacijom:
q = C V
C – Kapacitivnost provodnika
Grafički prikaz ove veze ima oblik prave linije koja počinje iz pocetka koordinatnog sistema i čiji je koeficijent pravca definisan kapacitetom provodnika.
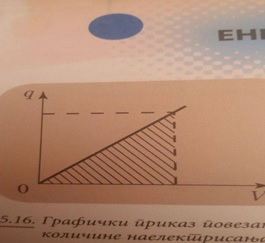
Površina ograničena datim vrednostima naelektrisanja i potencijala (šrafirani deo) brojno je jednaka radu električne sile, odnosno energiji električnog polja usamljenog provodnika.
Ae = Ee = 1/2 qV = 1/2 CV2 = 1/2 q2/C
Formula gustine energije električnog polja, odnosno energija po jedinici zapremine:
We = Ee/V= 1/2ɛE2