2. razred - Fizika

Kretanje fluida

Idealni fluid je neprekidna sredina koju odlikuju sledeća svojstva:

• ne postoji trenje među unutrašnjim slojevima (viskoznost)
• nestištljiv je.

Kretanje idealnog fluida krakterišu četiri osnovna makroskopska parametra:

• gustina
• pritisak
• temperatura
• brzina delića fluida

Delić se može poistovetiti sa česticom ali se u ovom slučaju razlikuje od razmatranja čestice kod idealnog gasa. Ovde se česticama smatra određena količina supstance čija se zapremina može zanemariti.

Najjednostavniji oblik kretanja fluida je stacionarno proticanje (strujanje) . Kod stacionarnog proticanja nema nagomilavanja delića fluida a ni vrtložnog kretanja.

Brzine kretanja fluida od tačke do tačke se mogu razlikovati. Kod stacionarnog kretanja u nekoj tački prostora brzine svih čestica koje prođu kroz tu tačku su jednake.

Linije (putanje) kroz koje se delići (čestice) fluida kreću zovu se strujne linije. Pri stacionarnom kretanju (strujanju fluida) strujne linije se poklapaju sa putanjama čestica i nigde se ne seku.

Deo fluida ograničen strujnim linijama zove se strujna cev. Čestice fluida koje se u nekom trenutnku nalaze u strujnoj cevi ne izlaze iz te cevi tokom kretanja.

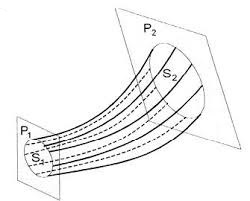
Jednačina kontinuiteta

Zakon u okviru njutnovske mehanike je zakon održanja mase.

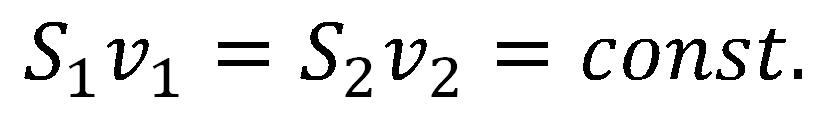
Pri čemu je:

• S₁ i S₂ - poprečni presek
• v₁ i v₂ - brzina protoka fluida

Predstavlja jednačinu kontinuiteta (neprekidnosti) za stacionarno proticanje idealnog fluida.

Jedinica protoka idealnog fluida je m³/s

Odnos brzina proticanja fluida kroz dva različita preseka cevi obrnuto je srazmeran odnosu površine tih preseka. Kroz presek veće površine brzina fluida je manja i obrnuto.

Bernulijeva jednačina

Pri stacionarnom proticanju idealnog fluida kroz strujne cevi ukupan pritisak, jednak sumi statičnog, dinamičnog i visinskog pritiska, ostaje neizmenjen (konstantan) u svakom poprečnom preseku strujne cevi.

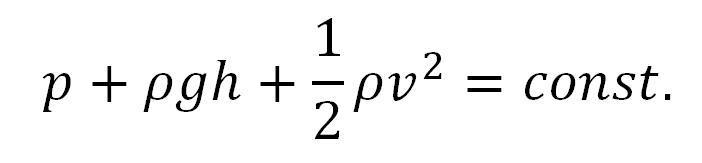
Tri dimenzije pritiska:

• p - statički pritisak
• ρ*g*h - visinski pritisak
• 1/2*ρ*v² - dinamički pritisak

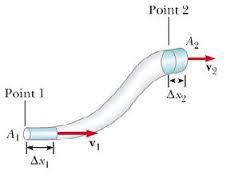
Primena Bernulijeve jednačine - Mlaznica

Posmatra se isticanje fluida iz posude kroz uzak otvor pod dejstvom pritiska.

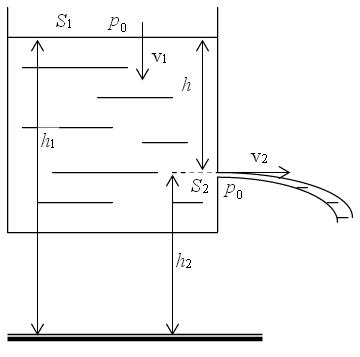
Bernulijeva jednačina: p + 1/2*ρ*v² + ρ*g*h = const.

Primena Bernulijeve jednačine na ovom primeru:

p₀ + 1/2ρv₂² + ρgh₂ = p₀ + 1/2ρv₁² + ρgh₁      (p₀ i p₀ se potiru):

1/2ρv₂² + ρgh₂ = 1/2ρv₁² + ρgh₁      Cela jednačina se deli sa ρ:

1/2v₂² + gh₂ = 1/2v₁² + gh₁      Ukoliko se izrazi v₂² dobija se:

v₂² = v₁² + 2gh₁ - 2gh₂      2h se izvlači ispred zagrade:

v₂² = v₁² + 2g(h₁ - h₂)      Sa slike je h = h₁ - h₂ :

v₂² = v₁² + 2gh

Sa slike na osnovu jednačine kontinuiteta se može napisati: S₁v₁ = S₂v₂

Pošto je: S₁ >> S₂ zaključuje se da je v₂ >> v₁ odnosno v₁ ≈ 0 brzina spuštanja nivoa tečnosti je približno nula.

Iz navedenog se dobija: v₂² = 2gh odnosno v₂ = √(2gh)

Primena Bernulijeve jednačine - Pitoova cev

Najjednostavniji oblik pitove cevi služi za određivanje brzine strujanja tečnosti u nekom otvorenom kanalu:

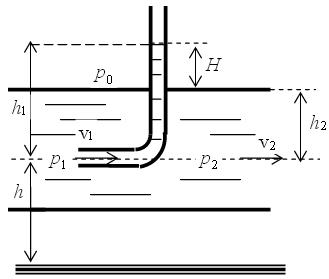
Bernulijeva jednačina: p + 1/2*ρ*v² + ρ*g*h = const.

Primena Bernulijeve jednačine na ovom primeru:

p₂ + 1/2ρv₂² + ρgh₂ = p₁ + 1/2ρv₁² + ρgh₁      na ulazu cevi tečnost miruje,

odnosno v₁ = 0 i statički apsolutni pritisci u datim tačkama iznose:

p₁ = p₀ + ρgh₁ i p₂ = p₀ + ρgh₂      zamenom v₁, p₁ i p₂ sledi:

p₀ + ρgh₂ + 1/2ρv₂² + ρgh₂ = p₀ + ρgh₁ + ρgh₁

izražava se član koji sadrži v₂

1/2ρv₂² = p₀ + ρgh₁ + ρgh₁ - p₀ - ρgh₂ - ρgh₂       +p₀ i -p₀ se potiru,

1/2ρv₂² = ρgh₁ + ρgh₁ - ρgh₂ - ρgh₂      cela jednačina se deli sa ρ:

1/2v₂² = gh₁ + gh₁ - gh₂ - gh₂      sabiraju se članovi:

1/2v₂² = 2gh₁ - 2gh₂      2g se izvlači ispred zagrade:

1/2v₂² = 2g(h₁ - h₂)      pri čemu je sa slike H = h₁ - h₂:

1/2v₂² = 2gH odnosno: v₂ = √(2gH)